Elżbieta Kasperska, dr hab inż., Silesian University of Technology, This email address is being protected from spambots. You need JavaScript enabled to view it., ul. Kaszubska 23, 44-101 Gliwice.
Elwira Mateja-Losa, dr inż., Silesian University of Technology, This email address is being protected from spambots. You need JavaScript enabled to view it., ul. Kaszubska 23, 44-101 Gliwice.
Rafał Marjasz, mgr, Silesian University of Technology, This email address is being protected from spambots. You need JavaScript enabled to view it., ul. Kaszubska 23, 44-101 Gliwice.
Abstract
The aim of our paper is to present the new results of research work on optmizaton and simulaton for some logistc problems in the company. The System Dynamics (SD) method and the Vensim simulaton language are applied in order to solve specifc managerial problems described by Forrester in the model of supply chain. The historical model of Customer-Producer-Employment System by Forrester (Forrester, 1961) has not been examined with the sensitvity analysis, from the “automatc” testng perspectve. Optmizaton experiments have not been conducted, either. It is surprising, since the model is old and widely known. The opportunites offered by the Vensim language allow us to perform such analysis. The visualizaton called “confdence bounds“ is used, to show the behaviour of chosen variables over a period of tme. The Monte-Carlo method is applied for sampling a set of numbers from within bounded domains (distributon for each searching parameters is specifed). The authors of this paper conducted numerous experiments in this scope. This paper presents their results and offers some conclusions formulated at the end.
Keywords: System Dynamics, sensitivity analysis, optimization, Vensim.
Introducton and literature review
The problem of sensitvity analysis and optmizaton performed on complex, nonlinear, dynamical and multlevels systems is very interestng from the methodological point of view, especially in the area of System Dynamics (SD). System Dynamics (Coyle, 1977, 1994, 1996, 1998, 1999; Forrester, 1961, 1969, 1971, 1972, 1975; Kasperska, 1995, 2002, 2003, 2005; Radosiński, 2001; Sterman, 2002; Wąsik, 1997, 1983) was developed in the late 1950’s and early 1960’s at the Massachusets Insttute of Technology’s Sloan School of Management by Jay W. Forrester. The approach can be applied to dynamics problems arising in complex social, managerial, economic or ecological systems. The main purpose of System Dynamics is to try to discover the “structure” that conditons the observed behaviour of the system over tme. System Dynamics tries to pose “dynamic” hypotheses that endogenously describe the observed behaviour of system.
In the area of System Dynamics method, there have not been much theory or practce related to combining simulaton and optmizaton. Although the frst trials were sufciently long ago (Keloharju, 1977, 1980, 1983; Winch, 1976), the fact is that incorporaton or embedding simulaton to optmizaton (and vice versa) has not been as popular as it should be in our view. Probably one of the main reasons was the lack of effectve tools. Popular sofware packages originally used in SD modelling and simulaton, did not offer possibilites of automatc optmizaton (for example: languages DYNAMO, DYSMAP (Kasperska and Mateja-Losa, Słota, 2006). Only such packages as COSMIC and COSMOS and Vensim (Ventana, 2007) make it possible to connect simulaton and optmizaton. Hence some papers published in the feld of SD (e.g. Coyle, 1996, 1998), though the work on this subject is stll scarce. The authors of this paper have some experience with the so-called embedding simulaton in optmizaton and vice versa, having conducted numerous experiments on DYNBALANCE family of models (Kasperska, 2005, 2009; Kasperska and Mateja-Losa, 2005, 2006; Kasperska, Mateja-Losa and Słota, 2000, 2001, 2003, 2006; Kasperska and Słota 2003, 2005, 2006).
The SD models usually contain several parameters. It is interestng to examine the effect of their variaton on simulaton output. We select some parameters and assign maximum and minimum values along with a random distributon over which to vary them to see their impact on the model behaviour.
Vensim has a method of setng up such sensitvity simulaton. Monte Carlo multvariate sensitvity works by sampling a set of numbers from within bounded domains. To perform one multvariate test, the distributon for each specifed parameter is sampled, and the resultng values are used in a simulaton. When the number of simulatons is set, for example, at 200, this process will be repeated 200 times.
In order to perform sensitvity simulaton, the user needs to defne what kind of probability distributon values for each parameter will be drawn. The simplest distributon is the Random Uniform Distributon, in which any number between the minimum and maximum values is equally likely to occur. The Random Uniform Distributon is suitable for most sensitvity testng and is selected by default. Another commonly-used distributon is the Normal Distributon (or Bell Curve) in which the value near the mean is more likely to occur than the values far away from the mean. The results of sensitvity testng can be displayed in different formats. Time graphs display behaviour of a variable over a period of tme. The variables spread values which combine to form individual simulaton traces.
Research method
The object of the experiments is the model named “Customer – Producton –Employment”, described in the literature by Forrester (1961) and Łukaszewicz (1975). The authors of this artcle used the descripton of the model, abbreviatons for parameters and variables afer Łukaszewicz. Our intenton is not to present the model, which is well-known, but to draw the reader’s atenton to the sensitvity and optmizaton experiments. In our paper we suggest the process of “automatc” sensitvity analysis and optmizaton by Vensim.
Analysis and study
Presentaton of the object of the experiments and the assumptons of the simulaton
Figure 1 presents the structure of the model “Customer – Producton – Employment” in Vensim conventon.
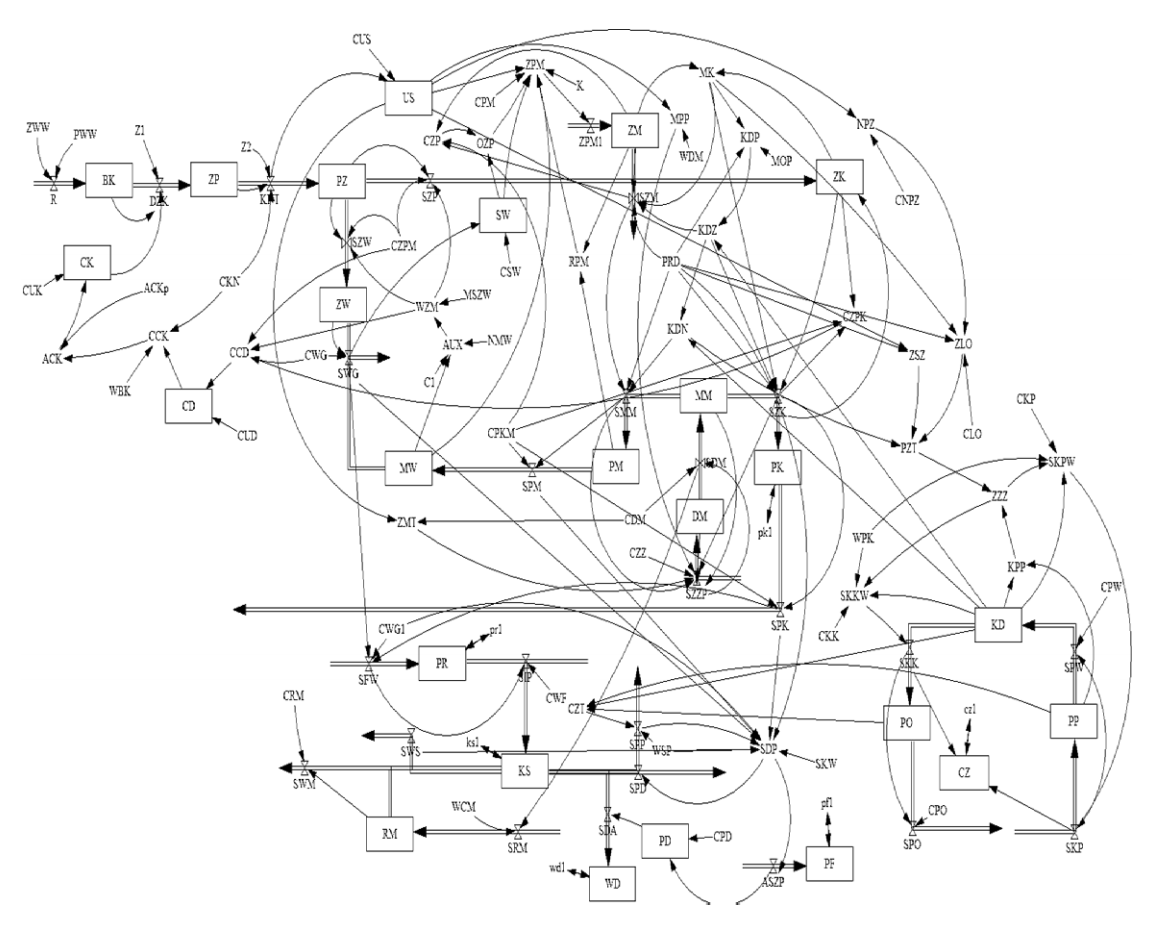
Source: Authors’ research, on the basis of Łukaszewicz (1975).
Table 1 presents the assumptons of the simulaton of the above model.
| Name of levels | Inital value of level | Name of parameters | Inital value of parameter |
|---|---|---|---|
| Order Filling, Inventory Reordering | |||
| PZ | 1000 | K | 4 |
| ZW | 700 | CUS | 15 |
| MW | 4000 | CSW | 2 |
| US | 1000 | CWG | 1 |
| SW | 700 | CZPM | 1 |
| CPM | 6 | ||
| Manufacturing | |||
| ZM | 2800 | PRD | 2.66 |
| ZK | 1200 | CPKM | 6 |
| PM | 4200 | MOP | 1 |
| PK | 1800 | ||
| Material Ordering | |||
| MM | 6000 | WDM | 6 |
| DM | 3000 | <CDM/td> | 3 |
| Labor | |||
| KD | 375 | CPO | 4 |
| PP | 0 | CKK | 10 |
| PO | 0 | CPW | 3 |
| CZ | 0 | WPK | 0 |
| CNPZ | 4 | CLO | 20 |
| Customer Ordering | |||
| BK | 30000 | CKN | 3 |
| ZP | 3000 | CUD | 4 |
| CK | 30 | CZPM | 1 |
| CD | 4.7 | CPKM | 6 |
| CWG | 1 | ||
| Cash, Proft and Dividends | |||
| KS | 10000 | WSP | 80 |
| PR | 50000 | CWG1 | 100 |
| RM | 6000 | WCM | 20 |
| PD | 20000 | CRM | 3 |
| PF | 0 | SKW | 50 |
| Source: based on Forrester (1961) and Łukaszewicz (1975). | |||
Results of the experiments on sensitvity analysis and optmizaton for some logistcs problems in the company
There are numerous logistcs problems in the “Customer – Producton – Employment” model. We would like to draw the reader’s atenton to some of them.
Problem number 1 – Too long tme of delivery from Producer to Customer. To conduct this experiment we selected the parameters: “CUD” (Time to Adjust Quoted Delivery at Factory), “CZPM” (Delay in Clerical Processing at Factory), “CWG” (Delay in Shipping at Factory), and observed the confdence bounds for variable “CD” (Delay in Quoted Delivery at Factory). The results are presented in Figure 2.
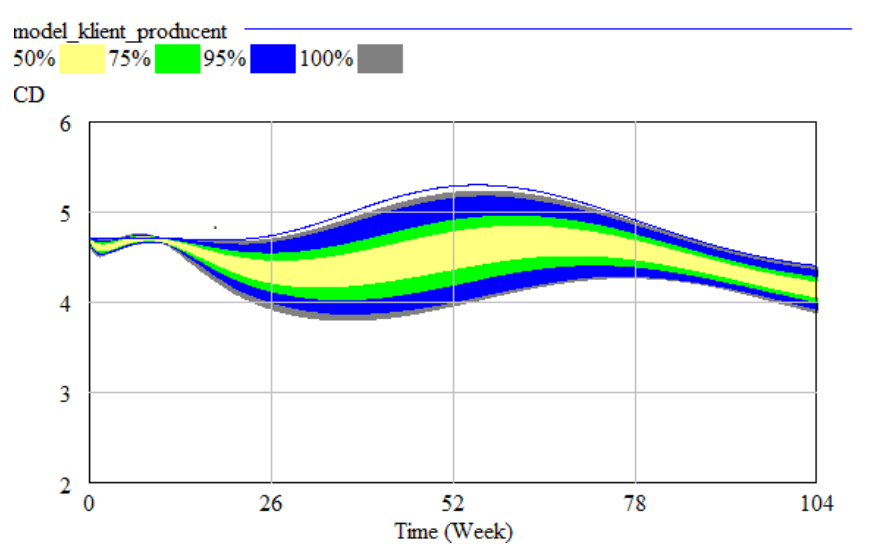
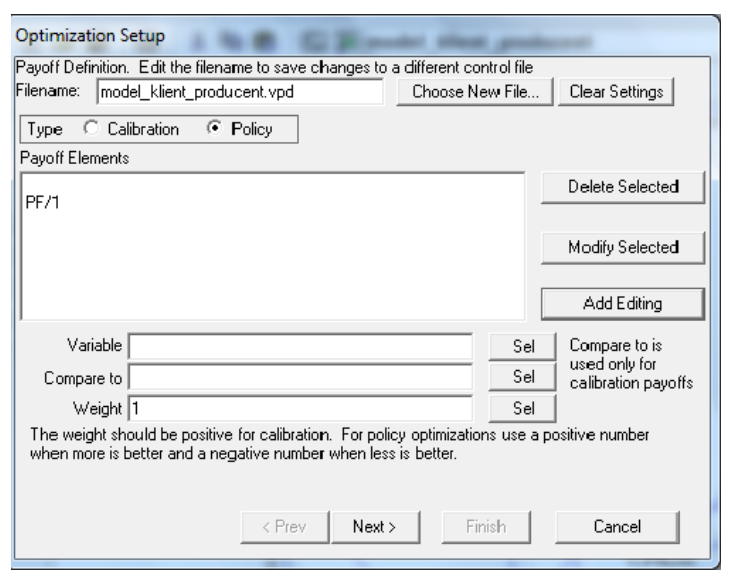
Our aim was to shorten the “CD” tme”. So we planned the optmizaton experiment consistng in minimizaton and used the optmizaton setup by Vensim, which is shown on windows on Figures 3 and 4.
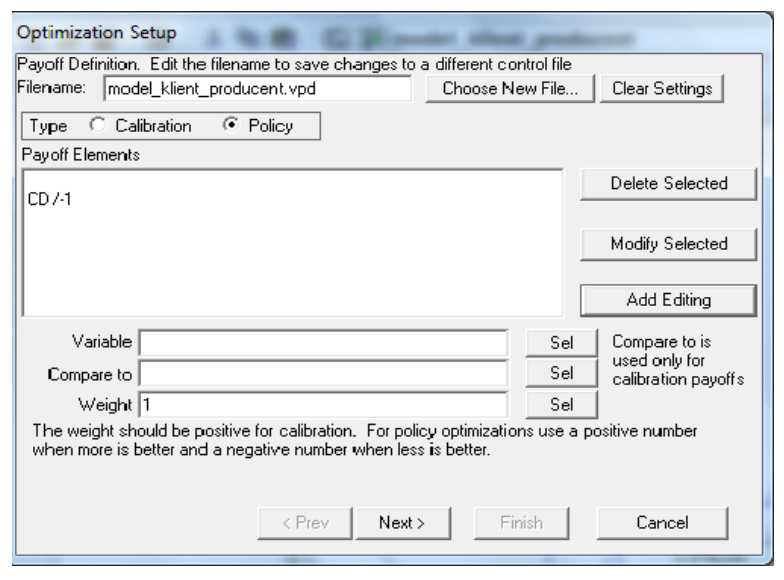
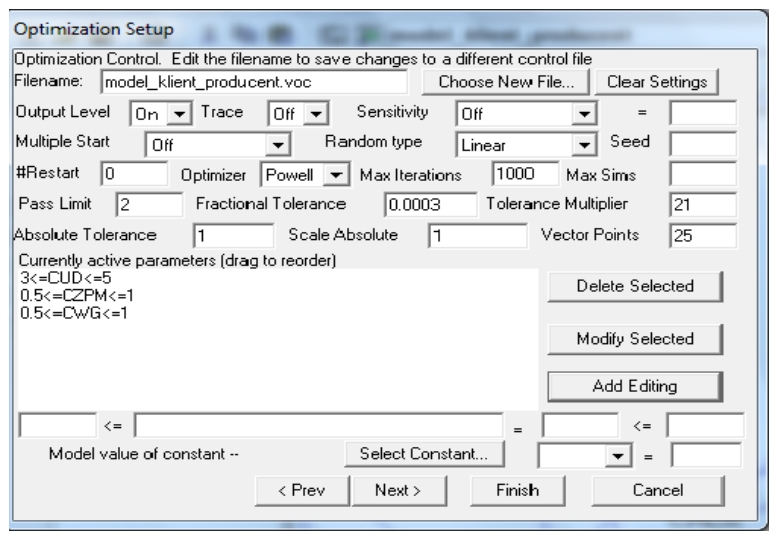
The results of the experiment are presented in Table 2.
The second problem is: Too large fluctuatons of labour level in the company.
To conduct this experiment we selected the parameter “CLO” (Time for Backlog Adjustment at Factory), and observed the confdence bounds for variables: “KD” (Producton Workers at Factory), “CZ” (Total Labour Change at Factory). The results are shown in Figures 5 and 6.
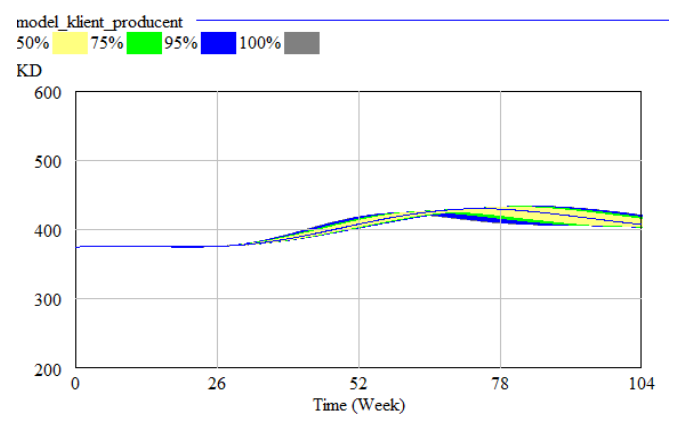
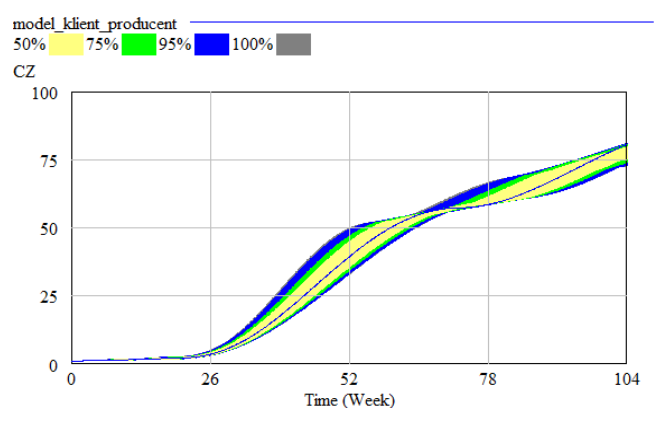
Our aim was to shorten the “CZ”. As above we planned the optmizaton experiment, consistng in minimizing the value of that variable. The results of the experiment are presented in Table 2.
The third problem is: Too large fluctuaton of “KS” level (Cash Balance at Factory).
To conduct this experiment we selected the parameter “CWG1” (FinishedGoods Price at Factory), “SKW” (Standard Inventory Cost per Item at Factory), “WSP” (Wage Rate at Factory), “PRD” (Productvity of Labour at Factory). The observed confdence bounds for net proft are demonstrated in Figure 7.
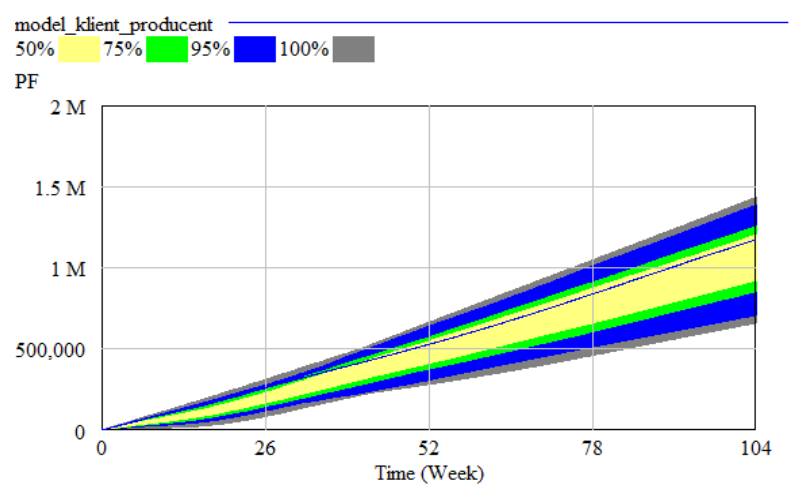
Our aim was to maximize “PF” (Net Proft Rate at Factory). We conducted the optmizaton by Vensim (see: windows in fgures 8 and 9). The results are presented in Table 2.
| Problem (no.) | Type of optmizaton (MIN, MAX) | Scope of parameters | Optmized values of parameters | Objectve functon Inital value Final value |
|---|---|---|---|---|
| 1. | MIN | CUD є (3,5) | CUD=3 | CD=4.89912 |
| CD=4.2645 | ||||
| CZPM є (0.5,1) | CZPM=0.545774 | |||
| CWG є (0.5,1) | CWG=0.595165 | |||
| 2. | MIN | CLO є(10,30) | CLO=30 | CZ=3845.9 |
| CZ=3285.4 | ||||
| 3. | MAX | CWG1 є (90,100) | CWG1=100 | PF=1.286e+006 |
| PF=1.417e+006 | ||||
| SKW є (45,50) | SKW=45 | |||
| WSP є (70,80) | WSP=80 | |||
| PRD є (2,2.66) | PRD=2 |
The possibilites of such experimentatons are practcally unlimited, however, the scope of our paper does not allow to extend the analysis.
Discussion of results
The comparison of the inital and fnal values of objectve functons in Table 2 allows us to ascertain that the choice of parameters and their scope was quite good, since the value of objectve functon has improved in all considered cases. The interestng fact is that the choice had “local” meaning (in the sense that parameters were from the sectors that were similar to objectve functons).
Łukaszewicz (1975) ascertains that in large scale models there are few sensitve parameters and a lot of insensitve parameters. It is vital to detect those sensitve parameters and thus improve the behavior of the system. Naturally the ‘trial-and-error’ process is tme and labor-consuming. This sensitve analysis by Vensim allows us to estmate the sensitveness of selected variable for the choice of given parameters in an easier way and prepare the basis for optmizaton process.
It should be stressed that the obtained results are in line with specifc assumpton about the characteristcs of the model entrance. Łukaszewicz in his paper (Łukaszewicz, 1975) recommended that the analysis of the model behavior should be under a wide spectrum of entrances, not only the classic “step” functons (like in our case) but the sinusoidal or linear ones (for example: trapezium). In books of Forrester (1961) and Łukaszewicz (1975) there are many examples of the analysis using the “trial and error” method. As a result of such analysis, the model behavior has been improved. In our paper we suggest the process of “automatc” sensitvity analysis and optmizaton by Vensim. Obviously, this simulaton language was not known by Forrester or Łukaszewicz, and their results of simulaton were tme and labor-consuming, and impressive in their tmes.
Conclusion
Firstly, we would like to draw a number of theoretcal conclusions:
- as Jackson (2006) said: “creatve holism is necessary in the modern world. Managers are facing ever increasing complexity, change and diversity, and the solutons they have at their disposal to cope with these issue are inadequate”. Thus we can say that the possibilites presented by SD are adequate for solving logistcs problems in the frm.
- simulaton – optmizaton experiments, on System Dynamics models allows to fnd sensitvity parameters and consequently conduct the search for optmal soluton for mult-criteria problems (objectve functons are modelled like inner elements of the model, with feedback in its structure),
- searching for optmal solutons can take into consideraton different preferences of decision makers (different form of objectve functon, with possibilites of weightng parameters for their factors).
- Secondly, we would like to offer some practcal conclusions:
- logistcs problems in the frm can be investgated using sensitvity analysis and optmizaton by Vensim,
- the Vensim language should become popular in the environment of System Dynamics modellers, because it is an effectve tool for such experiments as: simulaton – optmizaton: its sensitvity and optmizaton setups allow almost automatc search for confdence bounds or optmal value of objectve functons,
- doing simulaton with complex, large scale models, requires seeking many versions of structures, many parameters (especially sensitve parameters), including random elements. All of this is offered by Vensim. Moreover, a new version of this language (see: Vensim 2013) allows its users to create interactve games. This consttutes a new directon of future investgatons for the authors.
References
- Coyle, R.G. (1977). Management System Dynamics. Chichester: John Wiley & Sons.
- Coyle, R.G.(1994). Cosmic and Cosmoc. User Manuals. Londyn: The Cos-mic Holding Co.
- Coyle, R.G. (1996). System Dynamics Modelling. A Practcal Approach. Londyn: Chapman & Hall.
- Coyle, R.G. (1998). The practce system dynamics: Milestones, lessons and ideas from 30 years’ experience. System Dynamics Review, 14 (4), 343-365.
- Coyle, R.G. (1999). Simulaton by repeated optmisaton. Journal of the Operatonal Research Society, 50, 429 – 438.
- Forrester, J. W. (1961). Industrial Dynamics. Cambrigde: MIT Press.
- Forrester, J. W. (1969). Urban Dynamics. Cambrigde: MIT Press.
- Forrester, J. W. (1971). World Dynamics. Waltham, MA: Pegasus Communicatons.
- Forrester, J. W. (1972). Principles of Systems. Cambrigde: MIT Press.
- Forrester, J. W. (1975). Collected Papers of Joy W. Forrester. Cambrigde: MIT Press.
- Goncalves, G. (2009). World behaviour modes, pathways and overall trajectories, eigenvector and eigenvalue analysis of dynamic systems. System Dynamics Review, 25(1), 35-62.
- Jacson, M. C. (2006). Creatve holism: A critcal systems approach to complex problem situatons. System Research and Behavioural Science, 23, 647-657.
- Kasperska, E. (1995). Symulacja komputerowa dla wspomagania podejmowanych decyzji gospodarczych w przedsiębiorstwie przemysłowym o produkcji ciągłej. Nowe kierunki badań. Organizacja i Kierowanie, 2, 65-70.
- Kasperska, E. (1995). Badania symulacyjne na modelu SYMODREAL (model zakłóceń dostaw i produkcji zakładu przemysłowego). In: J. Bendkowski (Ed.), Zarządzanie przedsiębiorstwem przemysłowym. Problemy, metody, techniki. Gliwice: Wydawnictwo Politechniki Śląskiej.
- Kasperska, E. (2002). Cybernetc Formulaton of Some Functons of Management – Types of Simulaton and Optmizaton Approaches within the System Dynamics Method. Proceedings of the 20th Internatonal Conference of the System Dynamics Society, Palermo, Italy. July 28 – August 1. P. I. Davidsen, E. Mollona, V. G. Diker, R. S. Langer, J. I. Rowe (Eds.).
- Kasperska, E. (2003). System Dynamics Method and Supportng Decisions in Economic Organizaton. Proceedings of the 7th Conference of Internatonal Society for Decision Support Systems. DSS in the Uncertainty of the Internet Age. Katowice, Poland. July 13-16. T. Bui, H. Sroka, S. Stanek, J. Gołuchowski (Eds.).
- Kasperska, E. (2005). Some Remarks About Chosen Structural Aspect of System Dynamics Method. 6 éme Congrées Européen de Science des Systémes, AFSCET, Paris, France. September.
- Kasperska, E. (2005). Modelling Embedded in Learning the Acceleraton of Learning by the Use of the Hybrid Models on the base of System Dynamics Paradigm. In: T. Porębska-Miąc, H. Sroka (Ed.) Systemy Wspomagania Organizacji. (pp. 410-417). Katowice: Wydawnictwo Uniwersytetu Ekonomicznego.
- Kasperska, E. (2009).Metodologia budowy i wykorzystania modeli ewolucyjnych w aspekcie uczenia się (w) organizacji społeczno-gospodarczej. Gliwice: Wydawnictwo Politechniki Śląskiej.
- Kasperska, E., & Mateja-Losa, E. (2005). Simulaton Embedded in Optmizaton - a Key for the Effectve Learning Process in (about) Complex, Dynamical Systems. Proc. of the 5th Internatonal Conference, Atlanta, USA. May. (Eds.): V. S., Sunderman (et al.). Berlin: Springer.
- Kasperska, E., & Mateja-Losa, E. (2006). Extended Sensitvity Analysis of Parameters and Structure in System Dynamics Models - Some Case Study. Proc. of the 24th Internatonal Conference of the System Dynamics Society, Nijmegen, The Netherlands. July. (Eds): A. Grossler (et al.). New York: The System Dynamics Society.
- Kasperska, E., Mateja-Losa, E., & Słota, D. (2000). Some Extension of System Dynamics Method – Theoretcal Aspects. Proc. of the 16th IMACS World Congress, Lausanne, Switzerland. August 21-25. M. Deville, R. Owens, (Eds.).
- Kasperska, E., Mateja-Losa, E., & Słota, D. (2001). Some Dynamics Balance of Producton via Optmizaton and Simulaton within System Dynamics Method. Proc. of the 19th Internatonal Conference of the System Dynamics Society, Atlanta, Georgia USA. July. J. H. Hines, V. G. Diker, R. S.Langer, J. I. Rowe, (Eds.), New York: The System Dynamics Society.
- Kasperska, E., Mateja-Losa, E., & Słota, D (2003). Optmal Dynamical Balance of Raw Materials – Some Concept of Embedding Optmizaton in Simulaton on System Dynamics Models and Vice Versa. Proc. of the 20th Internatonal Conference of the System Dynamics Society, Palermo, Włochy. July 28 – August 1. P. I. Davidsen, E. Mollona, V. G. Diker, R. S. Langer, J. I. Rowe, (Eds.). New York: The System Dynamics Society.
- Kasperska, E., Mateja-Losa, E., & Słota, D (2006). Comparison of Simulaton and Optmizaton Possibilites for Languages: Dynamo and Cosmic and Cosmos – on a Base of the Chosen Model. Computatonal Science - ICCS 2006. 6 th Internatonal Conference reading, UK, May 28-31. Proceedings. Pt 1. V. N. Aleksandrov G. D. van Albada, P. M. A. Sloat, J. Dongarra (Eds.). LNCS 3991. Berlin: Springer.
- Kasperska, E., Mateja-Losa, E., & Słota, D (2006). Modelling and Simulaton of the Organizatonal Changes Using System Dynamics Method - Some Case Study. Cybernetcs and systems 2006. Proc. of the Eighteenth European Meetng on Cybernetcs and Systems Research, Vienna, Austria. Robert Trapp (Eds.). Vienna: Austrian Society for Cybernetcs Studies.
- Kasperska, E., & Słota, D. (2003). Two Different Methods of Embedding the Optmizaton in Simulaton on Model Dynbalance (2-2). Proc. of the 21st Internatonal Conference of the System Dynamics Society, New York, USA. July. P. I. Davidsen, E. Mollona, V. G. Diker, R. S. Langer, J. I. Rowe, (Eds.). New York: The System Dynamics Society.
- Kasperska, E., & Słota, D. (2005). Modelling of the Evoluton in the Structures, by the Use of Hybrid Models on the Base of System Dynamics. Proc. of the Conference of System Dynamics and Management Science: Sustainable development of Asia Pacifc, Shanghai, China. November 4 to 6. (Eds.): Q. Wang (et al.).
- Kasperska, E., & Słota, D. (2005). Optmizaton Embedded in Simulaton on Models Type System Dynamics - Some Case Study. Proc. of the 5 th Internatonal Conference, Atlanta, USA. May. (Eds.): V. S., Sunderman (et al.). Berlin: Springer.
- Kasperska, E., & Słota, D. (2006). Parallel Dual Problem of Optmizaton Embedded in Some Model Type System Dynamics. Proc. of the 24th Internatonal Conference of the System Dynamics Society, Nijmegen, The Netherlands. July 23-27. (Eds.): A. Grossler (et al.). New York: The System Dynamics Society.
- Keloharju, R. (1977). System dynamics or super dynamics. Dynamica, 4, 26-43.
- Keloharju, R. (1980). General frame of resources structure and trade off. Dynamica, 6, 9-20.
- Keloharju, R. (1983). Archiving structural sensitvity by automatc simplicaton. Dynamica, 9(2), 60-66.
- Łukaszewicz, R. (1975). Dynamika systemów zarządzania. Warszawa: PWN.
- Plate, R. (2010). Assessing individuals’ understanding of nonlinear causal structures in complex systems. System Dynamics Review, 26 (1), 19-33.
- Radosiński, E. (2001). Systemy informatyczne w dynamicznej analizie decyzji. Warszawa: PWN.
- Sterman, J, D. (2000). Business Dynamics – System Thinking and Modelling for a Complex World. Boston: Mc Graw-Hill.
- Sterman, J, D. (2002). All models are wrong: Reflectons on becoming a system scientst. System Dynamics Review, 18(4), 501-531.
- Wąsik, B. (1977). Modelowanie dynamiki systemów gospodarczych. Kraków: Wydawnictwo Akademii Ekonomicznej.
- Wąsik, B. (1983). Elementy dynamiki systemowej dla ekonomistów. Kraków: Wydawnictwo Akademii Ekonomicznej.
- Ventana Systems, Inc. (2007). Vensim User’s Guide Version 5. Ventana Simulaton Environment.
- Ventana Systems, Inc. (2013). Vensim Version 6.1. Ventana Simulaton Environment.
- Winch, G. W. (1976). Optmizaton experiments with forecast bias. Dynamica, 2(3), 107-116.





