Kazimierz Śliwa, Dr Hab. Kazimierz Śliwa, Uniwersytet Rzeszowski w Rzeszowie, This email address is being protected from spambots. You need JavaScript enabled to view it..
Abstract
The article concerns the problem of languages used in modeling and solving problems. Its framework stems from the distinction between two problem solving approaches – expert and interactive approach. The language choice is particularly important for the latter; we cannot solve a problem using a language that has not been used for the problem description. The text presents some arbitrarily chosen problem modeling languages, including computer supported ones. Special attention is paid to the SEQUAL and System Dynamics language.
Keywords: problem modeling and solving, formal modeling languages, expert and interactive approach to problem modeling, SEQUAL, System Dynamics language.
Introduction
It is possible to discern two types of problem solving and modeling. The first one, commonly used in problem modeling practice, relies in transferring the responsibility for a problem to external experts who – after diagnosing the problem – work out a suitable model, run it, and propose viable solutions. That approach has been dominating for decades, particularly in dealing with complex problems, and we call it alienative modeling hereafter. The nature of another approach is participative; it requires all people having an interest in solving a problem to be engaged in its modeling and solving. The term „interest” means problem stakeholders for whom the problem is part of their surroundings.
The dominance of the alienative approach dates back to the 1960's; works conducted at Wharton School, MIT, or Brookings Institution led to the creation of complex econometric models of whole national economic systems containing thousands of equations. What was the practical value of those models?
In general, these complex models and their usage had led to increasing disappointment with their practical implications. Forecasts provided by these models, despite their size and complexity, did not prove true; that is why as early as in the 1970's concerns regarding further development of these models began arising. Many critical comments indicated that these models do not have stable structure, and consequently, even small changes in the problem contents require the whole model to be re-worked. Another criticism pointed to the confusion between relationships and correlation; models were functional as far as the assumption about correlation among their components was true. Discovering relationships among problem variables is the core concept for problem modeling and solving - correlations does not always mean causality yet.
Under those circumstances a new approach to problem modeling has arisen. Although still in the initial development stage, participative modeling strives for acknowledging that problem solving is also learning about problem structure, discovering its structure and searching for leverage points existing within the structure. Problem solving domain, traditionally assigned to experts, had to be taken away from them and replaced with an open access to modeling of all involved stakeholders. Open access to problem solving and modeling creates many issues and a good part of them is linguistic – participation in problem solving depends on precise yet understandable for non experts language that would make it possible to work on problems collectively. Such a language must satisfy three requirements:
- expressiveness (the possibility of a formal description of the problem without losing its complexity and dynamics),
- clarity (ability to understand, create and modify a model by the participants),
- solvability (availability of methods for solving the model, especially the computer procedures).
If the modeling of problems, including the problem of regional development, is not to be exclusively the domain of experts, it is necessary to pose and solve the problem of modeling language. Not only do we describe the reality in our natural language, but also the way we see and understand the reality is embedded into our language. Using our natural, native language for problem modeling would be an ideal solution, yet it seems unreachable – it does not satisfy conditions mentioned above. It may be worth mentioning that the bigger the gap between natural language and the language of modeling, the greater the loss of precision of the model and its quality.
The line of argument adopted here is subordinated to this issue. At the beginning of the analysis, the generative and modeling role of spoken language is presented; then we describe the main types of languages used in the problems modeling and analyze the compatibility between the model and computer simulation. The model of a problem requires a series of operations to tackle the problem modeled through computer simulation. Without this condition problem inference is speculative and the practical value boils down to often complex but lacking practical advantages intellectual experiment. For this reason, another part of the study examines the simulation as an integral part of problem solution. and finally- the last part is devoted to the presentation of one of the most attractive alternatives in modeling – System Dynamics.
Language and problem solving
Language itself is a very dynamic system, not only in the sense that its social practice continuously modifies its forms and contents, but also that its use is associated with the intensive information processing that occurs in the brain. Elman indicates (Elman 1995), with this cognitive point of view, that this process may be something different than it is claimed by psychology. Language is an abstract representation of the reality surrounding us; its specific components can be arranged according to a variety of patterns and they create a semantic whole encompassing the situations in which we live. Traditionally, such representations were treated as a static entity, whilst the language is not a set of abstract symbols, but rather a multiplicity of meanings of space among which there may occur a variety of transitions. Some of them take place with relative ease, others with less, but generally the most difficult is the transition from one space to the other space and not within those spaces themselves (see Churchland & Sejnowski, 1992). For each space there may be a different linguistic identity – thus a different language. Therefore, mathematics has its own language, poetry uses another one, arts – painting or music have yet others. Our spoken language used in everyday practice is characterized by still other properties. To illustrate this imagine that we want to express using our natural language the music of Ludwig van Beethoven's Ninth Symphony or present the theory of gravity with a musical recording.
Linguistics and its relative science – semiotics, analyze the structure, the correctness and effectiveness of the language on three levels. The first level is semantics, dealing with the relationship between language constructs (characters) and objects of reality to which they relate; semantics, thus, takes care of binding the language to its origin (reality). Semantics affects our cognition in quite complex form. There is a feedback loop between the reality and language: we create only those constructs and meanings which have their counterpart in reality and – on the other hand - only the objects of reality that already exist in the existing repertoire of meaningful constructs (or are very close to them) are seen.
Another component of semiotics, syntax, designs formal structures of the relationship between the characters which make up the language by creating rules and their variations (e.g., grammar). The result is a set of propositional structures by which we describe reality in a way that is understandable to all speakers of that language. And finally, we have pragmatics – the study of the influence upon human behavior generated at the level of semantic and syntactic meanings. This is the most dynamic part of language, because we constantly create the meaning and interpretations of reality; they are not fixed but subject to constant change which requires learning process - reinterpreting the meanings, creating new ones – in short, the formulation of new theories of action.
Therefore, there are three areas through which our cognitive process muddles through while designing our understanding of the reality and actions aiming at it. The effectiveness of our action, the scope and character of changes produced by our behavior, depends on our crossing these areas with new meanings, rules, language.
What is the place of modeling in this picture? What linguistic dilemmas must be recognized and resolved? One will be here with reference to the graphic interface instilled into a language; such language - like no other – is an easy way to handle knowledge about the structures of the problems. This problem will be discussed further. Figure 1 presents above argumentation.
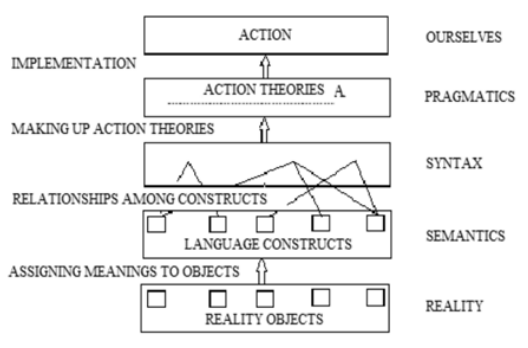
The key question here concerns the alternatives for the location of the modeling process in the context of language semiotics. It seems that these alternatives are:
- modeling language is a separate and specially created entity; it is an autonomous entity and although it can be analyzed in a similar semiotic perspective, its features make it inaccessible to other people. It seems that this choice is close to the aforementioned alienative approach to modeling and solving problems: language is hermetic, only we understand it, thus the possibility of criticism is reduced or eliminated.
- modeling language is merely an add-on to our natural language; it is an additional link of the semiotic structure of language that connects us to reality and there are valid reasons to believe that specialized expertise in modeling language is not necessary for modeling and solving problems.
It is helpful to support our argumentation with the paradigm reported as the Physical Symbol System Hypothesis (Newell and Simon 1976, Simon 1980). In H. Simon's words, phrases and other elements of language remind the construction in the edifice - words and expressions (semantics) are the blocks and bricks, and the relationships and rules (grammar) act as cement connecting them. Using language and thinking through the language is like construction process where the result is a mental model of the problem. The mental model of the problem is the beginning of the modeling process and necessary condition for future action.
In summary, problem solving requires modeling, either formal or intuitive, and this should take place close to the knowledge and commitment of stakeholders for whom the issue is "natural". Expert modeling approach essentially excludes this condition, which later negatively affects the link between the solution of the problem and the practical actions of the stakeholders. For these reasons we propose the use of modeling within the context of the stakeholders' collective knowledge, and that creates significant demands for precise and collaboration - orientated modeling language.
Some remarks on modeling languages
We assumed that the modeling language is a specially designed artificial system of signs and meanings, subject to certain interpretative rules and structure, which allows the expression of knowledge and information about the object being modeled in such a way that the object behavior has an interpretive meaning to the modeler. The practice of modeling has generated many languages, most of them are associated with software design and engineering programming.
Modeling languages are subject to the same rigors as the models and their prototypes. There are four main conditions that must be met:
- modeling language should allow visualization of the structure of the modeled system, both its current structure as well as the desired future structure,
- it should allow the description of the behavior of a modeled system,
- it should provide a template for the construction/modification of a modeled system, and:
- it should document decisions designed for influencing a system.
We propose below an arbitrary classification of modeling languages; they will be classified according to different criteria, such as user's interface, relation to a particular discipline of knowledge, descriptive character or formal mathematical notation. Graphical modeling languages are commonly used in project management and statistical decision theories. In software engineering graphical languages are particularly useful as they allow for the participation of various stakeholders; designing complex software should meet their expectations which often are expressed in natural language. Thus, graphical languages play an intermediate role between spoken, natural language and resulting software design. Another reason for gaining popularity is that graphical interface is understandable for most people so that even professionally unprepared participants can take part in the problem modeling process. This group of modeling languages is the most numerous.
Next group, algebraic modeling languages are most often high order programming languages and they are used to mathematically describe problems as equations system and solve them on a large scale. Typically, these are modeling languages for optimization problems, characterized by the availability of data and information as well as clearly defined structures. They typically do not contain any indication as to how make the model operate.
Behavioral modeling languages are used to describe the behavior of complex systems consisting of components that operate in a simultaneous manner. Although behavioral languages rely mainly on process algebra, their characteristic feature is the confinement only to observable phenomena that constitute the functioning of the system. They incline more towards descriptive languages than to modeling ones.
Modeling language of specific orientation can be divided into several groups depending on their purpose and the degree of structuring. Their common feature is a clear emphasis on software engineering in various stages of its design, which determine the type of language used. That group contains knowledge discipline oriented languages (called DspM), offering the library of concepts for each design stage and a special syntax, all in relation to the various stages of software development (discovery, analysis, design, architecture, testing). An example might be DspM SOMA (Service Oriented Architecture modeling) or SOMF (Service Oriented modeling Framework). Still other groups are domain-oriented languages (DSL), languageoriented context (DSF) and the object-oriented languages (OOML).
Especially the latter are worth attention because in many organizations they are applied to complex projects, where their essence is the involvement of numerous participants from many functional areas who otherwise would have difficulty with the participation. Object-oriented languages allow the creation of so called shared vision which is a collective wisdom enabling teams to strive for the same or similar goals. Another important feature of these languages is the extensive use of graphical interfaces and highly abstract codes of recording the contents and meanings. Although graphical access facilitates conceptual work on the project and the participation of interested persons, yet abstract code requires special preparation, thus the involvement of specialists is necessary.
And finally the last group of modeling languages has been developed primarily for modeling three-dimensional phenomena (e.g. space and structure of the WWW), and which is often referred to as virtual modeling languages. The prototype was Virtual Reality Markup Language (VRML) here, which in 1995 was replaced by the Virtual Reality modeling Language (VRML).
Table 1 shows our arbitrary classification of modeling languages, along with the main languages, which fall into any of the listed groups. It is worth noting the direction of evolution, which they were and still are subject to. Early practice of modeling problems were performed within the body of suitable scientific disciplines (e.g. algebra, econometrics) and modeling languages used were based on those disciplines to the extent that determines not only their tools, but also the domain of applicability. With the development of IT and computers for modeling and solving problems, the practice of modeling has been increasingly matching the needs of software designers and engineers (at the expense of other professional groups).
| GROUP | EXAMPLES |
|---|---|
| Graphical languages | Behavior Tree, Business Process modeling Language, Business Process modeling Notation, XML, EXPRESS EXPRESS-G, Extended Enterprise modeling Language, Flowchart, Fundamental modeling Concepts , iDEF (many versions, e.g. iDEF3, iDEF4, iDEF5), Jackson Structured Programming, Visual Design Description Language, Java, programming languages C, Object Role modeling, Petri Networks, Southbeach Notation, Specification and Description Language, Unified modeling Language, Architecture description language, AADL. |
| Algebraic languages | Algebraic modeling Languages, AiMMS, AMPL, GAMS, LPL, MPL, OPL and OptimJ |
| Domain orientated languages | Unified modeling Language, MetaEdit+, Actifsource, GEMS, GME, EAST-ADL, Energy Systems Language |
| Object orientated languages | LePUS3, interface Definition Language, ObjecTime Limited, Core Meta-Model, Paradigm Plus, |
| Behavioural languages | Behavior modeling Language, Universal modeling Language |
| Context depending languages | Framework Specific modeling Language, Rebeca modeling Language |
| Virtual languages | Virtual Reality modeling Language, Virtual Reality Markup, Generative Modeling Language, Web Services modeling Language |
Over the time a computer program has become the archetype of modeling; it is eventually a collection of routine, procedures, and algorithms telling computer what, how, and when to perform those instructions. From the viewpoint of modeling, a problem originates the instructions and the software is only a structural and functional replica of the problem that is to be solved. Such a significant impact of software engineering upon problem modeling has resulted in a progressive vertical and horizontal integration of modeling languages. Horizontal integration depends on opening a language to other modeling domains that have so far remained in another particular scientific discipline (e.g. econometric modeling - econometrics and optimization – mathematics). This has led to increased versatility of modeling languages. With horizontal integration the same language, depending on its properties (semantics, syntax and pragmatics), can model various fragments of the reality.
Vertical integration concerns the internal development of modeling languages. Many of them have already passed the stage of autonomous development, in which each language produces more advanced modeling tools, thus expanding their applicability and helping the horizontal integration. The strive for an universal language has taken different forms; in some cases languages collapse and integrate the properties of many languages into one of them. In others, languages have followed a common standard enabling to use more than one modeling language within the same problem scope.
The problem of language selection to a specific problem is a very complex issue. In this paper we formulated the idea that modeling complex problems, especially complex in terms of their structure and size (number of variables), requires an interactive and collective process, because active involvement of stakeholders in the process of modeling is the critical success factor, facilitating subsequent solution of the problem and its smooth implementation. For this reason, the choice of modeling language should be dictated by the quality of this language, which consequently leads to subsequent quality of the model itself. Among the existing proposals the concept of SEQUAL by Krogstie (2002) is worth mentioning. Figure 1 shows the general structure of SEQUAL.
A detailed discussion of SEQUAL exceeds the scope of this study and is probably not necessary. The name SEQUAL is an abbreviation of "semiotic quality" and its core concept emphasizes - in addition to the sufficiency and appropriateness of modeling language - the social efficiency of the modeling problem (and this is the central thesis of this paper). Sufficiency and appropriateness of language is reflected in te possibility to capture and present the structure and behavior of problems, while the technical efficiency is its adaptation to existing system requirements (e.g. IT solutions). Technical efficiency enables automatic verification and validation of the model, which requires its translation into a computer simulation (capability to generate a suitable computer code).
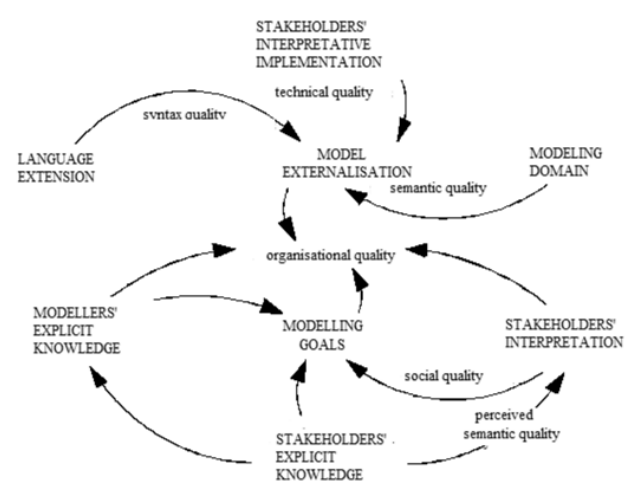
Source: Based on Krogstie 2002.
From modeling to simulation. The language of System Dynamics
While the modeling problem is the presentation of its variables, relationships existing among them (problem structure), and resulting problem behavior in the accepted formal modeling language, the next step of solving the problem - a simulation - requires codified procedures translating the problem model into computer procedures and operations. It is a mapping problem to a computer environment, which also requires a separate code (language). It seems that in the simulation of problems three main approaches exist:
- Discrete modeling
- Agent Based modeling, and
- Systems Dynamics modeling
Selecting one of them is of utmost importance, because each of these approaches accentuates different properties of a problem. Many decades of practical problem solving have granted rights to solve problems to experts in the area, ignoring other factors that could and should help choosing an appropriate approach to modeling. We accept in this paper that problem contents should determine the choice of the problem modeling approach; thus, it is not experts' expertise domain but the nature of the problem rather that should point to one of the three approaches.
Consider, for example, simple yet possible scenarios for economic growth. When consumer demand is growing, national production grows, and consequently, it is growing the demand for workforce securing the continuation of production at the required level. Consequently, manufacturing and service sector expand, generating demand for money and credit. Banking sector profit soars and the banks are willing grant more credit to the investment hungry sectors. Booming investment and consumption lead to the creation of the strengthening mechanism among the manufacturing, service, and financial sectors. Nevertheless, no system can grow without limits; a correct model of this problem should clearly show that mechanism and predict its failure.
Depending on the election of the approach we have different ways to model this scenario. The discrete modeling might assume that the existing market segments and consumers are "discrete" entities (events), and the labor force, businesses, and banks are available resources. Discrete in this context refers to the state identifiable behavior (ability to distinguish one state of the operating behavior of others and the ability to describe these states). Thus, problem behavior is represented as a chronological sequence of events where each event occurs at an instant in time and marks a change of state in the system. As the simulation mode is adjusted to those events the problem behavior (tendency over time) must be to great degree the continuation of previous behavior patterns. However, the extrapolation does not tell us much about the future of described system.
If we accept the subjective perspective of modeling (Agent-Based), the consumers and their behavior might depend, for instance, on marketing, market features, credit availability, and the processes of communication among all market actors. All those autonomous agents interact and the agent-based modeling attempts to assess their effects on the system as a whole. We may expect, therefore, that the complex feedback loop closing from the market and financial sector back to the corporations and consumers will be removed; again, in this case the prediction must be incomplete and short-term.
Finally, in the perspective of System Dynamics we should turn the attention to various feedback loops that can occur in this situation; for example, increased demand for loans increases their price, loans become more expensive, so the demand must decrease and people already repaying loans are starting to have trouble servicing them. This will lead to further constraint of market demand, and consequently, economic production slows down and the whole system reverts its behavior.
The success or failure of modeling complex problems (e.g. regional development) depends on understanding the relationships and internal dynamics produced by the components and the structure of a problem. Those relationships make up problem structure and determine its behavior. The policy or plan adopted for a problem is largely dependent on whether the policy makers truly understand the interaction and complexity of the system they are trying to influence. Considering the size and complexity of such problems, it is not surprising that the "intuitive" or "common sense" approach to policy design often falls short, or is counter-productive to desired outcomes. Besides, problem modelers must possess equally extensive and correct knowledge of the internal dynamics involved. It seems that out of these three approaches to simulation only System Dynamics provides suitable tools here.
Systems Dynamics was established as the modeling method in the 1950's and was developed by J. Forrester, then a professor at the Massachusetts Institute of Technology. The starting point was the transfer of the laws of physics to the field of economic, and later to social systems. Basic principles of system dynamics and features of its modeling language have been elaborated in the 60's. Attempts to use this method for modeling complex problems have proven its usefulness; it has successfully been applied to the analysis of macro-economic systems (the U.S. economy) and the regional development (under the name of Urban Dynamics). The former applications have resulted in a model explaining the long-term economic cycles of the U.S. economy, showing causes and contents of the Great Depression 1929 – 1933. In another and perhaps much more ambitious project System Dynamics was used to create a model of the world; apart of the original J. Forrester's version a number of its continuations have been produced by his students and colleagues (e.g. Denis and Donella Meadows). The usefulness of this method has caused that it was transferred to teaching in schools at all levels, both in the U.S. (so-called Project K-12) and in other countries, including Europe.
Presentation of System Dynamics as a methodology and modeling language should begin by sketching its ontological foundations. Ontological principles determine the way of understanding and modeling which affects the features of the language used. The language must capture the structure and behavior of systems exhibiting a dynamic changes over time. Therefore:
- an endogenous point of view should be adopted; the systems (problems) should be treated as closed in the sense that they can affect their input, so that the knowledge of their internal structure is sufficient to explain their behavior pattern; we assume that events are part of patterns, which are generated by problem structures,
- for understanding the structure it is necessary to identify relationships that exist between its elements; the most important type of relationships are those that create feedback loops- positive are responsible for the processes of growth and decay, negative - for their equilibrium. Circular causality in the system is the heart of system dynamics,
- importance of the identification of those variables that can accumulate their value over time (stock variables) and flows that affect them. Stocks are the memory of the system, and sources of disequilibrium mechanism driving a system away from its equilibrium state.
- things should be seen from a certain perspective. Individual events and decisions are only surface phenomena that stem from an underlying system structure.
- a continuous view should be adopted - events and decisions are not clearly separated in time and space.
The model-building scenario described above is just one of many possible scenarios
The simulation of system dynamics models uses numerical methods that partition simulated time into discrete intervals of length „dt” and conduct the system through time one „dt” at a time. While numerical methods may be sophisticated, the simulation engine must be able to solve algebraic equations that appear in the models with algebraic loops. Unlike discrete event and agent-based models, system dynamics models are deterministic, unless stochastic pattern is chosen. Mathematically, a system dynamics model is a system of coupled, nonlinear, first order differential equations.
System dynamics suggests a very high abstraction level, and is positioned as a strategic modeling methodology. Although the language of system dynamics is very simple, thinking in its terms and on its level of abstraction is quite difficult and pose frequently a real challenge. As a matter of fact, the System Dynamics is not only a modeling language – it is first of all the way and language of capturing the reality surrounding us. Therefore, unlike other modeling languages, the System Dynamics is showing us how to interpret a problem in terms of its internal dynamics, what is our initial mental model explaining its dynamics, how to test its correctness and how to improve it, how to convert mental model into simulation model, run it, and perform operations aiming at finding its solution or solutions.
The chain of intellectual and computer operations linking the reality with final solutions is quite complex, however. Let us use a classical example from J. Forrester's seminal book „Urban Dynamics”. Part of the city growth model presented there is the problem of land and housing facilities in the context of the construction industry. There is a fixed area of available land for construction. New buildings are constructed while old buildings are demolished freeing space for newer housing. We are interested in modeling and simulation of the main variable here – the number of buildings existing in the area and its change over time. Thus, it will be the primary variable of the problem.
Next step is the unleashing of our understanding that problem. Psychology has been coined very useful term here – mental model. A mental model is an explanation of our thought process about how the construction works operate. It is a representation of the relationships between its various parts as we intuitively perceive at the beginning stage of the modeling process. We all have mental models regarding all situations and problem we are involved in; in most cases story telling is the first and most natural way of conveying the knowledge about mental model. Based on this it is recommendable to identify other variables (influencing the primary one) existing in it.
Once we have the variables inventory, we proceed to reveal our assumptions about relationships existing between them. This is a critical point of the System Dynamics analysis as the statement “structure determines behavior” is probably the most important part of its ontology. It results in our initial understanding of the problem and its structure, preferably expressed with the causal diagram of the problem. Figure 3 presents one possible causal diagram of the construction problem.
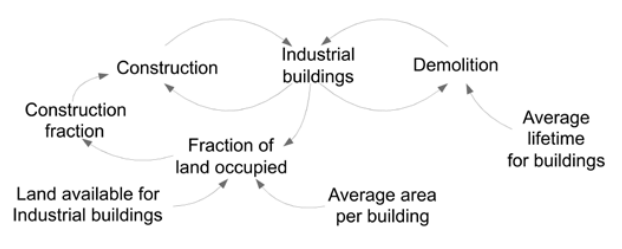
Source: Source: Based on Forrester 1969.
The veracity of the problem requires to see whether its structure can display the same or similar behavior pattern as in reality. That cannot be done unless we convert the causal diagram into simulation ready formal model. Each variable has an equation assigned to; what is interesting and useful for the System Dynamics software is that non measurable variables (like morale, motivation, knowledge, apathy, and so forth) can be included into a model and run. Figure 4 presents Construction and Land problem converted into the viable model
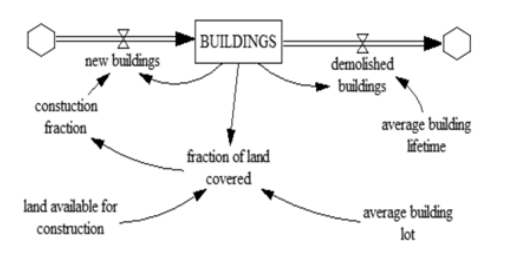
Variables definition (in terms of dependence)
- BUILDINGS = f(new buildings, demolished buildings)
- new buildings = f(construction fraction, BUILDINGS)
- fraction of land covered = f(BUILDINGS, land available for construction, average building lot)
- demolished buildings = f(average building lifetime, BUILDINGS)
- land available for construction; average building lot = constant variables
Source: based on Forrester 1969 (with Vensim TM)
Having had all variables defined we can check of the behavior patterns yielded by the model through the comparison with historical data. Simple behavior over time diagrams (BOT) do that; in case of significant discrepancies either our model structure or variables definition is incorrect and require changes.
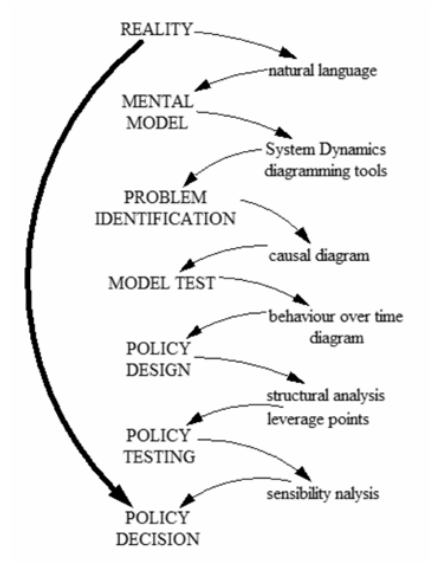
Once we obtain the problem model compatible with historical behavior pattern, we can proceed to the solution design process. System Dynamics rightfully claims that in order to change the problem behavior we should change its structure – structure determines behavior. Seeking problem solutions is thus a creative process of discovering those parts of the structure which to greater extent than other variables influence the behavior. These are so called „problem leverage points”; their control is the core concept of any policy design. Policy testing and sensibility analysis follow and they complete the problems solving through modeling and simulation cycle. Figure 5 shows this process.
References
- Churchland P. S., Sejnowski T.J (1992). The Computational Brain. Computational Neuroscience Series. Cambridge, MA: MIT Press.
- Elman J. L. (1995). Language as a dynamical system. In: Robert F. Port & T. van Gelder (eds.). Mind as Motion: Explorations in the Dynamics of Cognition. Cambridge, MA: MiT Press, 195-223.
- Forrester J. W. (1969). Urban Dynamics. Pegasus Communication, Portland.
- Krogstie J., Jørgensen H. D. (2002). Quality of interactive models. In: Olive A., Yoshikawa M., Yu E., (Eds). (2002). First international Workshop on Conceptual Modelling Quality (iWCMQ’02). October, Springer Verlag: Berlin 2002.
- Newell, A.; Simon, H. A. (1976). Computer Science as Empirical inquiry: Symbols and Search. Communications of the ACM, 3, 113–126.
- Simon, H.A. (1980). Cognitive science: The newest science of the artificial. Cognitive Science, 4, 33-46.






