Dr. Gordon G. Sollars, Department of Management, Fairleigh Dickinson University, Teaneck, NJ, 07666, This email address is being protected from spambots. You need JavaScript enabled to view it..
Dr. Sorin A. Tuluca, Department of Economics, Finance, and Internatonal Business, Fairleigh Dickinson University, Madison, New Jersey, 07940, This email address is being protected from spambots. You need JavaScript enabled to view it..
Abstract
The possibility of a frst-mover advantage arises in a variety of strategic choices, including product introductons, business start-ups, and mergers and acquisitons. The strategic management literature reflects ambiguity regarding the likelihood that a frst mover can or will capture additonal value. This paper uses a real optons approach to address the optmal tming of strategic moves. Previous studies have modeled real optons using either a perpetual or a European fnancial opton. With these models, a strategic choice could only be made either without respect to a tme frame (perpetual) or at a fxed point in tme (European opton.) Neither case is realistc. Companies typically have strategic optons with only a limited tme frame due to market factors, but companies may choose to act at any tme within that constraint. To reflect this reality, we adapt a method for valuing an American fnancial opton on a dividend paying stock to the real optons context. The method presented in this paper proposes a soluton for the optmum value for a project that should trigger a strategic choice, and highlights the value lost by not actng optmally. We use simulaton results to show that the tme frame available to make a strategic choice has an important effect on both the project value for when acton should be taken, as well as on the value of waitng to invest at the optmal tme. The results presented in this paper help to clarify the ambiguity that is found in the strategic management literature regarding the possibility of obtaining a frst-mover advantage. Indeed, a frst mover that acts sub-optmally could incur losses or at least not gain any advantage. A frst mover that waits to invest at the right tme based on the superior informaton supplied by models based on real optons could be beter positoned to obtain the benefts that might come from the frst move.
Keywords: first-mover advantage, strategic action, real option analysis, simulation, optimal investment, dynamic programming.
Introducton
The proper tming of strategic moves is widely discussed in the strategic management literature. The idea that a preferred value accrues to the “frst mover” in a sequence of strategic actons is reflected in the very terminology commonly employed: frstmover advantage (FMA) theory. The possibility of a FMA arises in a variety of contexts, including product introductons, business start-ups, and mergers and acquisitons. This paper uses a real optons approach to address the issue of the tming of strategic moves. We begin with a brief assessment of the theoretcal and empirical studies of FMA. In the next secton, we present a discussion of the idea of a real opton. Previous treatments of real optons typically have been restricted to optons that never expire (perpetual), or that only can be exercised at one point in tme (European). In the third secton, we present a technique that can be used to value an opton exercisable at any point in tme up to a fxed expiraton date (American). Subsequently, we use simulaton results from the technique to illustrate how the issue of FMA could be addressed. Finally, we offer a summary and conclusion.
In a classic study of FMA, Lieberman and Montgomery (1988) suggest three sources of advantage: (1) technology leadership, (2) asset preempton, and (3) buyer switching costs or uncertainty. In their model of the sources of FMA, Lieberman and Montgomery point to FMAs as endogenously generated by a combinaton of “frm profciency” and luck. In a subsequent treatment of FMA, Lieberman and Montgomery (1998) suggest that their earlier “profciencies” language be viewed through the lens of the resource-based view (RBV) of the frm (Barney, 1986; Prahalad & Hamel, 1990; Rumelt, 1987; Wernerfelt, 1984).
The key assumpton of the RBV is that frms in an industry have heterogeneous resources that are not perfectly mobile across frms (Barney, 1991). Here “resource” is very broadly construed to include anything that might conceivably add value to the frm. An implicaton of the RBV is that in order to expect to earn above-normal returns a frm must exploit resources already within its control (Barney, 1986). To the degree that the present control of relatvely immobile resources may be unrelated to new strategic intentons, Lieberman’s and Montgomery’s model inputs of frm profciency and luck tend to coalesce within the RBV. Although being a frst mover is considered to be a potental source of advantage within the RBV (Rumelt, 1987; Wernerfelt, 1984), simply as a mater of logic, some heterogeneous, relatvely immobile resources could lead to a frst-mover disadvantage.
Early empirical studies fnding FMA were conducted by the staff of the Federal Trade Commission, which found advantages in cigarete brands (Whiten, 1979) and prescripton drugs (Bond & Lean, 1977). Makadok (1998) found FMA for product introductons in the money market mutual fund industry. Lee, Smith, Grimm, and Schomburg (2000) found FMA in new product introductons by testng shareholder wealth effects in the telecommunicatons, computer, and brewing industries.
Complementng the sources of FMA are factors that suggest that a frst mover might suffer a disadvantage. In this regard, Lieberman and Montgomery (1988) list free-rider effects; technological uncertaintes or discontnuites; and “incumbent inerta” that could sap a frst-mover’s will to adapt to environmental changes. Theoretcal models support the idea that the value of being a frst mover is not unambiguous. For example, Suarez and Lanzolla (2007) present a model in which the pace of market and technology changes influences the likelihood of FMA. In the context of “product cannibalism”, a partcular subset of product introducton, Conner (1988) states conditons for the second mover to have an advantage.
Empirical studies also suggest that the frst mover does not always hold an enviable positon. Shankar, Carpenter, and Krishnamurthi (1998) conclude that a so-called “innovatve” late mover can outsell the frst mover. In the mergers-and-acquisitons context, Carow, Randall, and Saxton (2004) fnd that only the frst mover with “superior informaton” captures any advantage. Kalyanaram, Robinson, and Urban (1995) fnd that being a frst mover does not determine long-term industry survival.
Furthermore, a difcult challenge to studies purportng to fnd FMA is presented by the queston of the proper measure of performance. Lieberman and Montgomery (1988) express concern that empirical studies atemptng to address FMA are biased toward using market share, rather than proftability, measures due to the lack of disaggregated proft data. In a meta-analysis of 90 tests of FMA, VanderWerf and Mahon (1997) found that tests using market share were disproportonally more likely to fnd FMA than tests using proftability. Cui and Lui (2005) fnd no advantage in proftability in the pioneering of foreign investment in China. Using PIMS data, Boulding and Christen (2003) fnd a long-term proft disadvantage to the frst mover at the business unit level. Thus, even where FMA is found, no additonal value may have been created. In this paper, we assume that increasing frm value is preferred over simply increasing market share, an assumpton fully consistent with the real optons approach.
In summary, the strategy literature counsels cauton regarding the value of moving frst. However, even if contextual factors point to the desirability of being the frst mover, the decision maker in such a case stll faces the queston of exactly when to make the frst move. If analysis shows that there is litle value to be lost by waitng, then the frst move can be made at a tme that is in some sense optmal, and additonal value may be captured. A decision maker contemplatng a strategic choice could beneft from an analysis quantfying the value that could be gained or lost by actng or not within some tme frame. Concern over the possible loss of frst-mover status might be unwarranted.
To assist the making of this kind of tming decision, we present an approach for determining the optmal tming of a strategic choice using the theory of real optons. In this theory, strategic choices such as product introductons or mergers and acquisitons are analogized to the choice to purchase a fnancial optons contract. Although the idea of a “real opton” is not new, many managers remain unfamiliar with it. Furthermore, our methodology provides an approach that is more general in some respects than what is typically found in the literature. The next secton discusses the idea of a real opton, beginning with its origins in the theory of fnancial optons.
Real Optons
Arrow and Fisher (1974) provide the classic interpretaton of opton value in the context of an investment decision: the value of utlizing more informaton before making an irreversible choice. They show that this value is always nonnegatve. Henry (1974) is concerned with the same problem, but calls it the "irreversibility effect". The term coined by Arrow and Fisher (1974) was "quasi-opton value". This quasi-opton value is a measure of the worth of maintaining flexibility regarding when or whether to take some strategic opportunity.
The value of such an opton is very difcult to quantfy, and some would prefer to rely on qualitatve reasoning and intuiton when incorporatng flexibility into their strategies. Hayes and Garvin (1982) recommend the use of judgment when analyzing possible strategic actons, without subjectng it to the "distortons" of quanttatve methods. However, they were primarily concerned with the use of discounted cash flow valuaton, which is known to systematcally under value strategic choices. Although the limitatons of quantfcaton should not be ignored, intuitvely, the maintaining of strategic flexibility must have some cost. Furthermore, a quanttatve model may help identfy where, and what kind, of intuitons are needed. The real optons method we outline below is an example of such a model.
The task of quantfying the cost of flexibility became easier with the introducton of opton pricing models from fnance into corporate strategy. Mason and Merton (1985) are among the frst to formalize the use of optons pricing theory for the valuaton of strategic flexibility; they might have coined the term of “real optons” for such an exercise. The analogy between strategic choices and fnancial optons, that either may be taken (exercised) or not, is straightorward. However, the concomitant beneft of a theory for pricing fnancial optons, beginning with the Black-Scholes model (Black & Scholes, 1973), on strategic choices is substantal. Majd and Pindyck (1987) were among the frst to discuss the applicaton of real optons to the value of waitng before making an investment decision. Later, Dixit and Pindyck (1994) were the frst to apply a modern and rigorous approach to the problem of investment under uncertainty. They apply the concept of real optons to several investment strategies, using the idea of a perpetual fnancial opton to draw most of their conclusions. McDonald (1998), who makes an atempt to link rules of thumb to a more rigorous approach to investment decision rules based on real opton analysis, uses perpetual optons as well. Luehrman (1998a) and (1998b) atempts to demystfy the concept of a real opton using simple methodologies based on decisions that can be made only at specifed moments, which corresponds to a European fnancial opton approach. Even some of the more recent papers on the topic use perpetual optons to produce results and comparatve statcs (Lukas & Welling, 2012).
The American fnancial opton, which may be exercised at any tme before maturity, is a more realistc model of the flexibility inherent in strategic choices. In the next secton we present a technique for valuing a real opton of the American type. Following that, we demonstrate that relaxing the perpetuity or European opton assumptons in favor of the American leads to materially different conclusions regarding the value of waitng, and the optmal value at which a strategic opportunity should be taken.
Valuing an American-style Real Opton
Strategic flexibility is usually valued with the help of stochastc dynamic programming or stochastc control, both nonlinear problems in themselves. The frst refers to discrete tme models, while the later implies contnuous tme. Optmal behavior under uncertainty is described as a strategy (Lund, 1991) which defnes the decision variables at each point in tme as a functon of the history up to, and, including that point. The stochastc control problem is based on the dynamic programming principle and the Hamilton-Jacobi-Bellman equaton (Oksendal, 1991). The principle of dynamic programming (Dufe, 1988) states that the current value of a dynamic program is the maximum, over the set of possible current actons, of the current reward and the expected present value of the dynamic program over the next period.
When the variable of concern follows a Brownian moton, the dynamic problem leads to a parabolic partal differental equaton with a free boundary conditon. This problem does not have a closed-form soluton. In general, numerical methods and most analytcal approximatons will generate solutons where the degree of accuracy depends on the number of iteratons considered, as illustrated by Carr and Faguet (1994). Because the soluton has no closed form, intuitve interpretatons are usually not feasible.
To eliminate this complicaton, as mentoned earlier, most research has discussed various applicatons to real optons using the perpetual, or, sometmes, the European, opton. In the case of a perpetual opton, the partal differental equaton becomes an ordinary one, and fnding a soluton is a trivial mater. If we consider the case of real optons, the assumpton of perpetuity lacks realism simply because a strategic choice will not remain open forever.
Consider a decision maker, whether entrepreneur or corporate manager, who has the opportunity to take some strategic acton, which we will call, simply, a “project”. The conditons that have created this partcular project opportunity are not important. Any kind of resources or capabilites may be considered: superior technology, natural monopolies, patents, entrepreneurial insight, even corporate culture, to name a few. We adopt the following model (see Tuluca, 2000). The value of the project, P, today is P0 and can be regarded as the present value of some future cash-flows, discounted at rate ρ. The evoluton of the project value, P, is uncertain over tme. We assume that maintaining the flexibility concerning whether or not to take the project has a cost I0. Furthermore, the decision maker faces a tme limit, T, during which the choice to invest I0 must be made or the chance to take the project is lost. The use of the tme limit T accommodates two aspects of strategic choice. First, the conditons that enable the possibility of a strategic acton are unlikely to be maintained indefnitely. A patent or license may expire. A classic example is the concession on a natural resource, where resource exploitaton has to begin within some period of tme or the concession is lost. Second, compettors eager (or too eager) to capture any FMA may preempt the opportunity, as in the case of product introductons or mergers and acquisitons actvites.
At each tme t<T, the decision maker can chose to take the project or to postpone the decision in order to obtain more informaton about the evoluton of P. Let this decision be our control variable u. Obviously, it can take just two values, 1 or 0, which correspond to investng I0 or not taking the project. We designate by V the value at tme 0 of the acton to invest in the project at some future point in tme. V can be thought as the value of investng with the flexibility of waitng. V is given by:
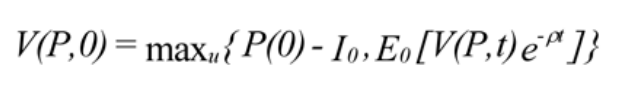
At tme zero, the value of investng in the project, V(P,0), is the maximum between the expected value of investng in the project at a tme t, discounted to the present at a rate ρ, and the value of taking the project at tme 0. Our maximizaton is governed by the control variable u, which in this case also represents our decision. From [1] it is clear that the value is always greater than or equal to zero. However, [1] is not helpful for solving the problem since no point in tme is specifed. A common technique is to rewrite [1] in two steps: one at tme t and another at tme t+ t. Equaton [1] is then writen as:
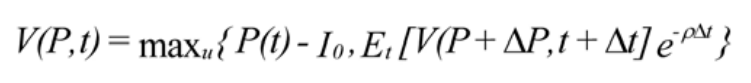
The new formulaton makes clear that the policy u that is chosen should be such as to be optmal for the future course of acton. The formulaton in [2] is the Bellman equaton, and represents a dynamic programming problem (see for example, Lund, 1991). The problem starts at the tme limit T and is worked backwards toward an optmal decision at tme 0. This is a maximizaton problem over the control u. The problem is without a soluton unless a process describing the evoluton of P, the project value, over tme is specifed. While many processes could be considered, the preferred specifcaton is a geometric Brownian moton with a drif. The assumpton of such a process can be sometmes unnecessary, but it is widely used in the literature.
The familiar form for the process describing P over tme is:
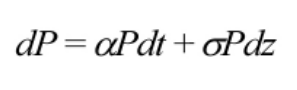
Where α is the rate of growth of project P, is the instantaneous volatlity, and dz is a Wiener process. To state the problem in contnuous tme, let t go to 0. The problem becomes:
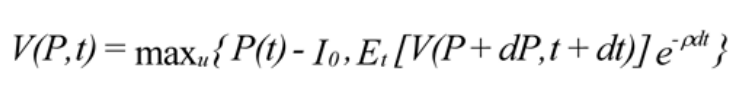
Expanding the second term on the right-hand side by Ito's Lemma[1] [5] yields:
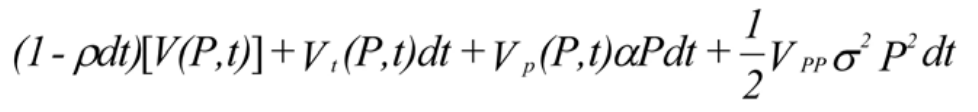
where terms going to 0 faster than dt are ignored. Substtutng into [4] and restatng the conditon imposed by the maximizaton and the frst term on the righthand side gives:
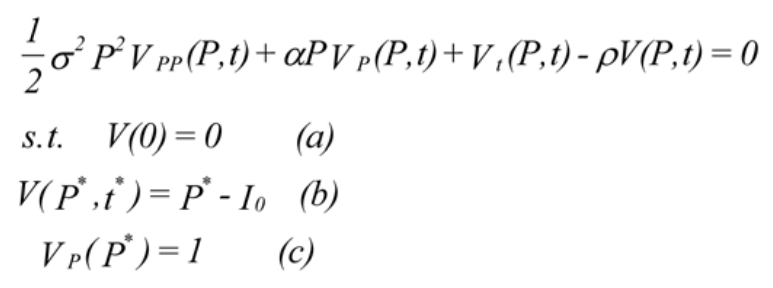
This restatement of the conditon acknowledges that at some point in tme a value could exist that will make the exercise of the opton, i.e., taking the project, optmal. In other words, there might be a point where our control u=1. Conditons [7b] and [7c] are known as "value-matching" (Dixit & Pindyck, 1994) and "high contact" (Merton, 1973) conditons. These authors make the following point: if a value P* for which the project is optmally taken, exists, then that value will be independent of the current value of P. Furthermore, when and if the now current value of P reaches P*, the value of taking the project now versus waitng is equal. Nothing further is to be gained by waitng.
Unfortunately the boundary conditon is free, and therefore a closed-form soluton does not exist. To analyze under what conditons the project should be taken before tme T is reached, we start by temporarily changing the boundary conditons. We will impose the constraint that the project cannot be taken before tme T. At such tme the value of the project is
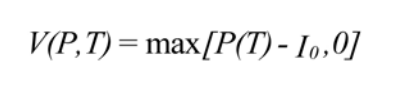
This becomes the new boundary condition for [7], replacing [7b] and [7c]. The explicit form can be found if we transform the expectation into an integral and substitute P as a solution for the differential equation [3]. The solution is now (Ingersoll, 1987, p 312):
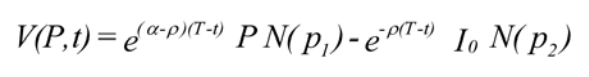
Here p1 and p2 are defined as:
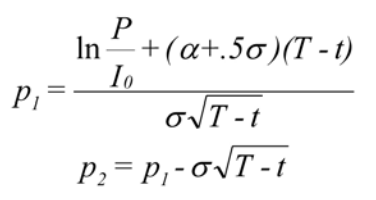
From this point the problem becomes one of finding a relationship between α, the growth rate of the project, and ρ, the discount rate used to solve the control problem. In the theory of financial options this is usually solved by adjusting the growth rate for the appropriate level of risk and then discounting by the risk free rate, r. This standard procedure is derived either from a no-arbitrage argument (Merton, 1973), or from an equilibrium model such as the Capital Asset Pricing Model (CAPM) (Black & Scholes, 1973; Sharpe, 1964).
The usual contention is that a market-traded asset, perfectly correlated with the project under consideration, can be found (McDonald & Siegel, 1984, among others). Once this crucial assumption is made, the standard option pricing model framework with a solution of the same type as [10] can be considered in order to find a solution. The growth rate α is replaced by r - δ, where δ is the return shortfall (McDonald & Siegel, 1984) of a non-traded asset, and ρ is replaced by the risk free rate. With this substitution, we face the classic problem of an option written on a dividend paying stock (see Merton, 1973). That there are only two cases where such a problem has a closed-form solution is well known: when either the option is European (it can be exercised only at a specified point in time); or when the option is perpetual and time disappears from the differential equation [7]. In the case of an American financial option (which can be exercised at any point in time until its maturity) the solution is a numerical or analytical approximation.
Despite the widespread acceptance of the “traded-asset" methodology for the evaluation of real options, the underlying assumption is problematic. A traded asset correlated with a future project is often, if not usually, impossible to find. In addition, the real option cannot really be traded[2]. When the decision maker has a real option, more often than not the project in question is a completely new idea for which no analogous asset exists. In this situation, the procedure of adjusting the project growth rate and then discounting by the risk-free rate is a misleading exercise. However, the derivation of [10] did not imply either the "no-arbitrage" argument or an equilibrium model of the CAPM genre. Therefore, [10] is still a valid solution for the real option problem of the value of waiting, when the option is of the European type. Even if, conceptually, financial and real options have their differences, the problems of valuing the two remain related since the solutions have the same general formula, when a closed-form formula can be found
When the real option can be exercised at any time before maturity, however, the solution given by [10] is no longer appropriate; rather, it is necessary to solve a system given by [7]. Barone-Adesi and Whaley (1987) (BAW) developed an interesting approximation for the solution of [7] in the case of an American financial option. Because of the similarity between the financial and real options the same procedure can be applied to determine the value of waiting to make a strategic choice.
The solution proposed by BAW provides several benefits. First, their approximation has the advantage of being computationally inexpensive and relatively simple enough to be understood by managers. The need to make the real option problem easier to understand and to offer a simpler formulation for managers has been recognized several times (Copeland & Tufano, 2004; Luehrman, 1998a, 1998b). Second, the optimum value of the project for when action should be taken is computed as part of the derivation, and therefore no separate algorithm for determining this value is needed. Third, even though only an approximation, the formulation in BAW holds up well when compared to more complex approximations. BAW compared their approximation with the implicit finite-difference method and the approximation proved to be quite accurate. A short summary of the BAW approximation is presented below.
Using BAW notational substitutions: M = 2ρ/σ2, N = 2α/ σ2, and τ = T – t, the time remaining to expiration from present, in place of t, the time evolving from time 0 to present the following is an approximate solution for [7]):
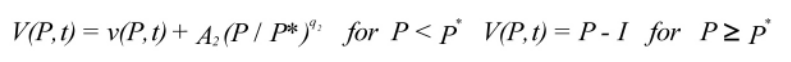
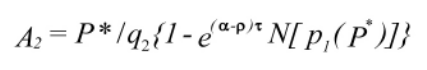
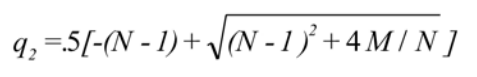
P* is the solution to the following implicit equation:
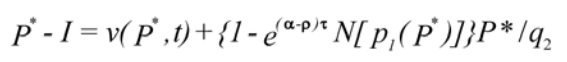
and ν(P,t) is given by:
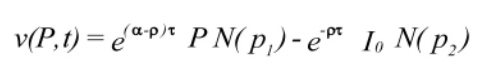
where p1 and p2 are defined as:
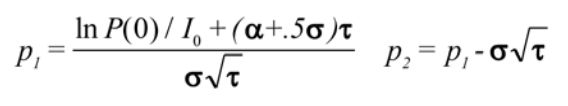
The BAW approximation allows a new insight into the real options problem of the value of waiting to make a strategic choice, thus providing a more realistic approach to the real world. At the same time, the value at which the project is optimally taken can be obtained as a by-product of the approximation. P* represents a “trigger” value for the decision whether or not to take the project. As the value of the project P evolves during time until T due to the availability of more information, should P ever become equal to, or exceed, P*, then the optimal time for action has been reached.
The real options methodology provides a way to value strategic flexibility. Having strategic flexibility could be misused, and therefore a favorable situation could be lost. Knowledge of the value of the real option and of the value of the project when this real option can be exploited at its maximum can provide the decision maker with vital information. The model proposed in this paper has three distinctive advantages over the previous literature in that it: (1) avoids the problem of finding a traded asset correlated with the project; (2) allows for an analytical solution of a real option with an American, as opposed to a perpetual or European, format; and (3) provides a solution for the optimum value for the exercise of the real option.
An objection could be raised to the validity of such an analysis in a setting where the rates of project growth and discount, as well as the volatility of P, are only subjective or intuitive judgments that are not subject to market verification. A counterargument can be made as follows. Consider a company valuing a variety of projects. If all of them are analyzed by the same decision maker, then the same subjectivity or intuition is applied to all the projects. Thus, from the perspective of the decision maker, the decision to take some over others can be optimal even if subjective. The fact that the analysis does not rely upon assets traded in the marketplace does not imply the decision is not optimal based upon the available information. The market is in no position to evaluate the real option the decision maker has, since most of the real options are on projects which are not public knowledge.
Real Options Perspective on FMA
This section presents some numerical examples that demonstrate the importance of the time constraint for understanding the value of strategic flexibility. Consider a project P with a current present value, P0, of $100 from all its future cash flows. The investment I0 necessary to take this project is also $100. Obviously, the ratio P0/I0 is 1. We will further assume a discount rate, r, of thirty percent. Let q be the difference between the discount rate r and the rate of growth a of the project, and σ be the standard deviation (volatility) of P. P* is the present value of all the future cash flows for which the project is optimally taken at a time t
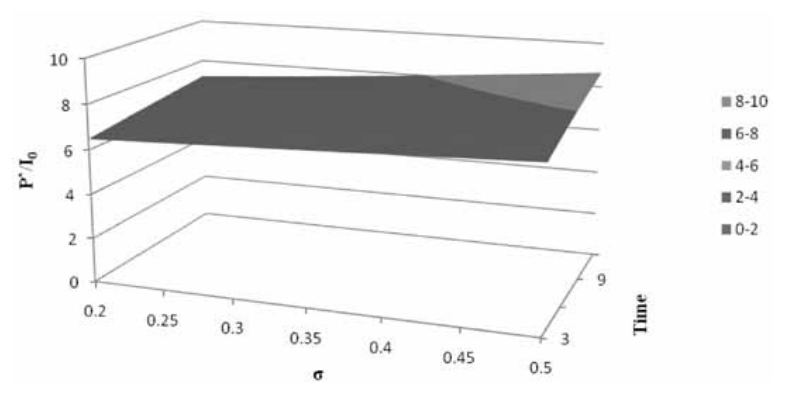
Table 1, Panel A varies the time limit T from three to twelve months, and q from .01 to .09, for a fixed σ = .35. For all values of q considered, the time to maturity has a direct relationship on P*/I 0. As the opportunity to take the project narrows, less and less value for P is required to trigger action. The ratio varies from about four to forty depending on the values of T and q considered. The time effect is not as powerful as the q effect. For instance, a doubling of time from six months to twelve months increases the value by 8% to 10% across q, while a doubling of q increases the effect on the value about two times. Nevertheless, Panel A shows the selection of a time limit T can influence the optimal value for taking the project. More importantly, it shows that use of the BAW method can quantify the effect of having the flexibility of choice in the time limit T.
Panel B shows the effect of varying both the time constraint of the option and the effect of volatility (with the value of q fixed at .05) on P*/I0. Here, the effect of the time constraint is not only comparable to, but even greater than, the effect of the volatility of the project. The range of both effects is between ten percent and twenty percent. The implication is that the time constraint could become more important than the effect of volatility for the value of P*. For instance, an increase in the time limit T, the time of expiration of the option, from three to twelve months has almost the same effect as an increase in uncertainty, as measured by the volatility of P from twenty percent to fifty percent. Most managerial decisions focus on uncertainty. Yet, this simulation provides evidence that the time frame available for action is equally important.
Given that the selection of the time limit T exerts an influence comparable to that of σ, the selection of T should be made with equal care. When dissimilarities between the traded-asset assumption and the real-world situation predominate, the value chosen for σ is a guess that must be based largely upon intuition. In that case, sensitivity analysis by varying σ can help to determine how closely σ must be known for its value to affect the strategic decision. To the degree that the time limit T on a strategic decision is flexible, the BAW method allows the sensitivity of the decision to be measured. Figures 1 and 2 summarize in a succinct way the sensitivities discussed in both panel A and panel B of Table 1.
A decision maker who initially calculates a relatively large value of P* relative to P0 has a reason to wait before committing to be the first mover. On the other hand, if P0 is already relatively close to P*, then little value might be placed at risk by acting immediately and seizing first-mover status. However, in order to assess this choice, the value of taking the project P with the flexibility of waiting, V, must be computed, as in Table 2 below.
| Panel A (constant σ=.35) | |||||
|---|---|---|---|---|---|
| q | |||||
| T | .01/th> | .03 | .05 | .07 | .09 |
| 3 | 34.13 | 11.36 | 6.81 | 4.86 | 3.78 |
| 6 | 36.26 | 12.05 | 7.21 | 5.14 | 3.99 |
| 9 | 38.18 | 12.66 | 7.6 | 5.37 | 4.16 |
| 12 | 40.02 | 13.23 | 7.88 | 5.59 | 4.32 |
| Panel B (constant q=.05) | |||||
| T (months) | |||||
| σ | 3 | 6 | 9 | 12 | |
| .20 | 6.48 | 6.74 | 6.98 | 7.22 | |
| .25 | 6.59 | 6.89 | 7.16 | 7.42 | |
| .30 | 6.70 | 7.05 | 7.36 | 7.64 | |
| .35 | 6.81 | 7.21 | 7.56 | 7.88 | |
| .40 | 6.93 | 7.38 | 7.77 | 8.13 | |
| .45 | 7.05 | 7.56 | 8.00 | 8.39 | |
| .50 | 7.17 | 7.74 | 8.23 | 8.67 | |
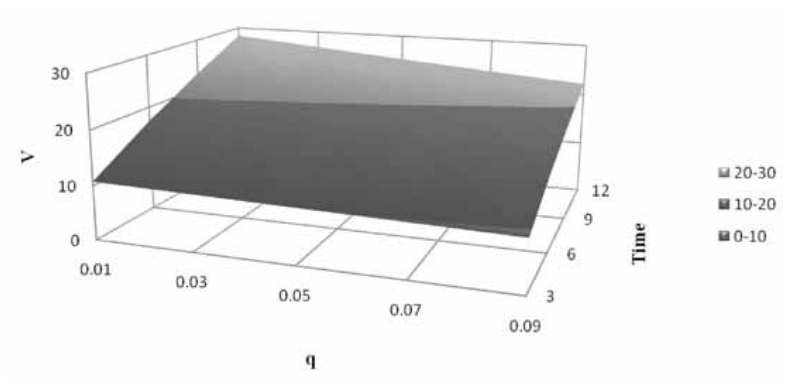
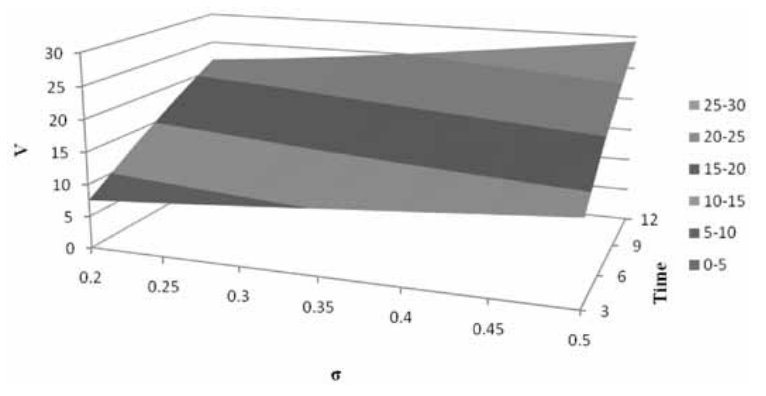
Table 2 presents the effects of varying time, along with the other two parameters, on V. Panels A and B show that the time constraint is much more important than the effect of q or σ. While increasing q increases the value of V fractionally, the time effect increases the value of V between two and three times. The same result holds when the effect of time is compared with the effect of volatility. Table 2 helps to quantify how having more time to make the decision can dramatically affect the value of the strategic action. That extending the time to expiration increases the value of the option is not new. However, that the time constraint has effects more powerful than those of uncertainty or the difference between the discount and the project growth rate has not been presented in the previous literature. Figures 3 and 4 show the sensitivity of V to T, q and σ.
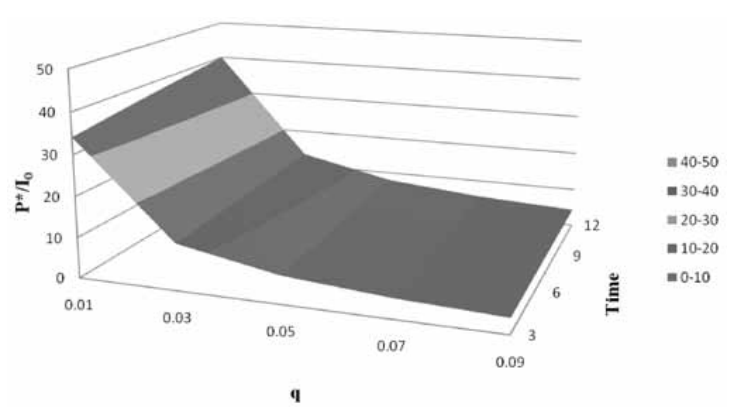
| Panel A (constant σ=.35) | |||||
|---|---|---|---|---|---|
| q | |||||
| T | .01/th> | .03 | .05 | .07 | .09 |
| 3 | 10.76 | 10.42 | 10.08 | 9.76 | 9.43 |
| 6 | 17.36 | 16.61 | 15.89 | 15.18 | 14.50 |
| 9 | 23.11 | 21.93 | 20.79 | 19.69 | 18.64 |
| 12 | 28.31 | 26.68 | 25.19 | 23.63 | 21.21 |
| Panel B (constant q=.05) | |||||
| T (months) | |||||
| σ | 3 | 6 | 9 | 12 | |
| .20 | 7.53 | 12.8 | 17.54 | 21.89 | |
| .25 | 8.34 | 13.74 | 18.49 | 22.79 | |
| .30 | 9.2 | 14.78 | 19.59 | 23.89 | |
| .35 | 10.09 | 15.89 | 20.79 | 25.12 | |
| .40 | 10.99 | 17.04 | 22.06 | 26.45 | |
| .45 | 11.9 | 18.21 | 23.37 | 27.84 | |
| .50 | 12.81 | 19.4 | 24.72 | 29.27 | |
The use of the BAW method in this context allows the effect, here on V, of the time limit T to be quantified. Table 1 suggests that there can be a penalty for the first mover being too eager and moving before P* is reached. Yet, the time constraint does not have much of an effect on the value of P*. Table 2 confirms that a first mover that moves before the optimal time could incur a great loss. The value to be lost by taking the project before P* can grow dramatically as T, the time limit for the decision, increases. To the extent that the time constraint is flexible, the value of the option from the gain due to waiting can be calculated, and a sensitivity analysis performed, as demonstrated in Figures 3 and 4.
Summary and Conclusion
The theoretical and empirical literatures of FMA are ambiguous regarding the likelihood that a first mover will obtain an advantage. Lieberman and Montgomery (1988) explain FMA as a function of firm proficiencies and luck. Subsequently, Lieberman and Montgomery (1998) tie their notion of firm proficiencies to the RBV of the firm. A fundamental of assumption of the RBV is that firms are able to gain competitive advantage only from resources they already happen to control (Barney, 1986). With theoretical studies highlighting the importance of luck and chance factors in attaining FMA, a method for quantifying the effects of timing on the value of a strategic decision with flexibility is welcome. Furthermore, some empirical studies point to the need for superior information in order to properly exploit first-mover status (Carow et al., 2004). We present a method for obtaining more information about the optimal time to take a strategic action. In some sense, our results validate Kalyanaram et al. (1995) who find that being a first mover does not determine long-term industry survival. Clearly, if the first mover does not move optimally, its long term survival could be compromised by the taking of a value-destroying project. While there is potential for an FMA strategy, it is not always the case that the potential is realized. Our results support, for instance, Shankar et al. (1998) who conclude that a so-called “innovative late mover can outsell the first mover. This is entirely possible if it is the late mover who takes the project at the optimal time.
To provide some quantitative grounding for optimal action, we use a dynamic programming approach to derive the value of a project with the option to wait for a fixed time limit. Using the analogy between the valuation of the project and the valuation of an American call, and exploiting the BAW approximate solution, numerical examples are provided. The examples show that the time to expiration of the right to take the project has a dramatic influence on the value of the project. This result, while implied by some previous earlier research (Ingersoll & Ross, 1992, for example), is usually not discussed in the literature. While previous research focused on the influence of either the interest rate (Ingersoll & Ross, 1992) or of uncertainty (Leahy & Whited, 1996), this paper highlights the importance of the time constraint with respect to the other two factors. The numerical and graphical simulations make obvious that the time factor has important implications for strategic choice.
Apart from this new result, we formalize a simple method of computing the value of projects with the option to wait, which at the same time provides the optimal value at which the project should be started. This can be a convenient tool for the valuing of new product introductions, mergers and acquisition, small business startups, or for use by patent rights holders (see Damodaran, 1996, for a simpler version of this example). Second, the approach is independent of the complications posed by the no-arbitrage or equilibrium conditions usually employed in financial options theory. Freedom from these assumptions makes sense in the entrepreneurial world of business startups and product introductions, where business intuitions concerning returns and uncertainty can play an important role.
References
- Arrow, K., & Fisher, A. (1974). Environmental Preservation, Uncertainty, and Irreversibility. Quarterly Journal of Economics, 88, 312-319.
- Barney, J. B. (1986). Strategic Factor Markets: Expectations. Luck, and Business Strategy. Management Science, 32(10), 1231-1241.
- Barney, J. B. (1991). Firm Resources and Sustained Competitive Advantage. Journal of Management, 17(1), 99-120.
- Barone-Adesi, G., & Whaley, R. (1987). Efficient Analytic Approximation of American Option Values. Journal of Finance, 42(2), 301-320.
- Black, F., & Scholes, M. (1973). The Pricing of Options and Corporate Liabilities. The Journal of Political Economy, 81(3), 637-654.
- Bond, R. S., & Lean, D. F. (1977). Sales, Promotion, and Product Differentiation in Two Prescription Drug Markets. U.S. Government Printing Office Retrieved from http:// www.ftc.gov/be/econrpt/197702salespromo.pdf.
- Boulding, W., & Christen, M. (2003). Sustainable Pioneering Advantage? Profit Implications of Market Entry Order. Marketing Science, 22(3), 371-392.
- Carow, K., Randall, H., & Saxton, T. (2004). Do Early Birds Get the Returns? An Empirical Investigation of Early-Mover Advantages in Acquisitions. Strategic Management Journal, 25, 563-585.
- Carr, P., & Faguet, D. (1994). Fast accurate valuation of American options. Working paper. Cornell University.
- Conner, K. R. (1988). Strategies for Product Cannibalism. Strategic Management Journal, 9, 9-26.
- Copeland, T., & Tufano, P. (2004). A real-world way to manage real options. Harvard Business Review.
- Cui, G., & Lui, H.-K. (2005). Order of Entry and Performance of Multinational Corporations in an Emerging Market: A Contingent Resource Perspective. Journal of International Marketing, 13(4), 28-56.
- Damodaran, A. (1996). Investment Valuation. Hoboken. New Jersey: John Wiley and Sons, Inc.
- Dixit, A., & Pindyck, R. (1994). Investment under Uncertainty. Princeton, New Jersey: Princeton University Press.
- Duffie, D. (1988). Security Markets: Stochastic Models. San Diego, California, HBJ Publishers: Academic Press.
- Hayes, R., & Garvin, D. (1982). Managing as if Tomorrow Mattered. Harvard Business Review, 60(3), 70-79.
- Henry, C. (1974). Investment Decisions Under Uncertainty: The "Irreversibility Effect". The American Economic Review, 64(5), 1006-1012.
- Ingersoll, J. E., Jr. (1987). Theory of Financial Decision Making. Lanham, Maryland: Rowman & Littlefield Publishers.
- Ingersoll, J. E., Jr., & Ross, S. (1992). Waiting to Invest: Investment and Uncertainty. Journal of Business, 65(1), 1-31.
- Kalyanaram, G., Robinson, W. T., & Urban, G. L. (1995). Order of Market Entry: Established Empirical Generalizations, Emerging Empirical Generalizations, and Future Research. Marketing Science, 14(3), 212-221.
- Leahy, J. V., & Whited, T. M. (1996). The Effect of Uncertainty an Investment: Some Stylized Facts. Journal of Money, Credit and Banking, 28(1), 64-83.
- Lee, H., Smith, K. G., Grimm, C. M., & Schomburg, A. (2000). Timing, Order and Durability of New Product Advnatages with Imitation. Strategic Management Journal, 21, 23-30.
- Lieberman, M. B., & Montgomery, D. B. (1988). First-Mover Advantages. Strategic Management Journal, 9, 41-58.
- Lieberman, M. B., & Montgomery, D. B. (1998). First-Mover (Dis)Advantages: Retrospective and Link with the Resource-Based View. Strategic Management Journal, 19, 1111-1125.
- Luehrman, T. A. (1998a). Investment Opportunities as Real Options: Getting Started on the Numbers. Harvard Business Review, 76(4), 51-67.
- Luehrman, T. A. (1998b). Strategy as a Portfolio of Real Options. Harvard Business Review, 76(5), 89-99.
- Lukas, E., & Welling, A. (2012). Negotiating M&As under uncertainty: The influence of managerial flexibility on the first-mover advantage. Finance Research Letters, 9, 29-35.
- Lund, D. (1991). Stochastic Models and Option Values: An Introduction. In D. Lund & B. Oksendal (Eds.), Stochastic Models and Option Values (pp. 3-18). Amsterdam: Elsevier Science Publishers B.V.
- Majd, S., & Pindyck, R. S. (1987). Time to build, option value and investment decisions. Journal of Financial Economics, 18(1), 7-27.
- Makadok, R. (1998). Can First-Mover and Early-Mover Advanatges Be Sustained in an Indusrty with Low Barriers to Entry/Imitation? Strategic Management Journal, 19, 683-696.
- Mason, S., & Merton, R. (1985). The Role of Contingent Claims Analysis in Corporate Finance. In E. Altman & M. Surahmanyam (Eds.), Recent Advances in Corporate Finance (pp. 7-54). Homewood, Illinois: Richard D. Irwin.
- McDonald, R. (1998). Real options and rules of thumb in capital budgeting. In L. Trigeorgis (Ed.), Innovation, Infrastructure, and Strategic Options. London: Oxford University Press.
- McDonald, R., & Siegel, D. (1984). Option Pricing When the Underlying Asset Earns a Below Equilibrium Rate of Return: A note. Journal of Finance, 39, 261-264.
- Merton, R. C. (1973). Theory Of Rational Option Pricing. Bell Journal Of Economics And Managemant Science, 4(1), 141-183.
- Oksendal, B. (1991). Stochastic Control Theory- A Brief Summary. In D. Lund & B. Oksendal (Eds.), Stochastic Models and Option Values (pp. 19-29). Amsterdam: Elsevier Science Publishers B.V.
- Prahalad, C. K., & Hamel, G. (1990). The Core Competence of the Corporation. Harvard Business Review, 68(3), 79-91.
- Rumelt, R. P. (1987). Theory, Strategy, and Entrepreneurship. In D. Teece (Ed.), The Competitive Challenge: Strategies for Industrial Innovation and Renewal (pp. 137- 158). Cambridge, MA: Ballinger.
- Shankar, V., Carpenter, G. S., & Krishnamurthi, L. (1998). Late Mover Advantage: How Innovative Late Entrants Outsell Pioneers. Journal of Marketing Research, XXXV(1), 54-70.
- Sharpe, W. F. (1964). Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance, 19(3), 425-442.
- Suarez, F. F., & Lanzolla, G. (2007). The Role of Environmental Dynamics in Building a First Mover Advantage Theory. Academy of Management Review, 32(2), 377-392.
- Tuluca, S. (2000). The Investment Decision: the Value of Waiting and the Time Factor. Paper presented at the May 2000 Industrial Engineering Research Conference, Cleveland.
- VanderWerf, P. A., & Mahon, J. F. (1997). Meta-Analysis of the Impact of Research Methods on Findings of First-Mover Advantage. Management Science, 43(11), 1510- 1519.
- Wernerfelt, B. (1984). A Resource-based View of the Firm. Strategic Management Journal, 5, 171-180.
- Whitten, I. T. (1979). Brand Performance in the Cigarette Industry and the Advantage to Early Entry, 1913-74. U.S. Government Printing Office Retrieved from http://legacy.library.ucsf.edu/documentStore/s/n/k/snk28e00/Ssnk28e00.pdf.
- If V is a function of P and t, Ito's Lemma says that V must follow a process described by:
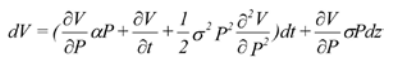
- Arguably in the mergers and acquisitions context the strategic options are “traded”, but the frequency of such trades is differs [5] greatly from the continuous time assumption that the option pricing model assumes.





